Author |
Topic: Ghost ships (Read 9104 times) |
|
Paul Hsieh
Guest
|
Nice problem. The way to see the solution, I believe, is just visualize the paths of the ship in 3 dimensions (where time is one of the dimensions) and realize that the 4 lines must be coplanar.
The ship captain has many alternatives to get off the plane. One way is to veer off in a purpendicular direction for a short time, then redirect to the target location. This will guarantee leaving the plane, thus missing "E".
|
|
 IP Logged |
|
|
|
tim
Junior Member
Posts: 81
|
 |
Re: Ghost ships
« Reply #1 on: Aug 5th, 2002, 10:18pm » |
 Quote  Modify
|
Better yet, just slow down or speed up. That way you still reach your destination without having to muck about with fiddly position estimations and compass bearings.
|
|
IP Logged |
|
|
|
Paul Hsieh
Guest
|
No, that's not good enough to get off the plane. Consider the possiblity that all the boats are on the same line running at different speeds, with F behind you running towards you and going a lot faster than you. You can still satisfy the original statement of the problem, and your strategy is not sufficient to escape a collision with F.
(Alternatively, F may be in your path ahead going really slowly with E and G coming towards you in the other direction ... etc.)
You really need to get off the plane. A change in direction while maintaining speed is sufficient, but just changing speed is not.
|
|
IP Logged |
|
|
|
tim
Junior Member
Posts: 81
|
|
Re: Ghost ships
« Reply #3 on: Aug 6th, 2002, 9:30pm » |
Quote Modify
|
No, my solution works.
Consider the ships as tracing out coplanar lines in a plane in 3-space (x,y,t). If the motion plane is not orthogonal to the t=0 plane, then varying velocity means that the ship leaves the plane. Yes, this leaves open the case where the plane is orthogonal to t=0.
However, we know that the motion plane is not orthogonal to t=0: G hit H amidships, rather than in the stern or bow, which means that G's velocity vector is not parallel with H's.
Hence varying speed without direction does mean that H leaves the plane.
Remember to read all parts of the problem. Sometimes seemingly insignificant words are more important than they appear 
|
|
IP Logged |
|
|
|
Chronos
Full Member
Gender: 
Posts: 288
|
|
Re: Ghost ships
« Reply #4 on: Aug 15th, 2002, 5:52pm » |
Quote Modify
|
It somewhat bugs me that this riddle requires the captain of H to break the rules. It says right up front that all ships pursue their course steadily, changing neither direction nor speed. If Capt'n H can't change his direction or speed, then there's really nothing meaningful that he can do. If, contrary to the problem statement, he can change his velocity, then why should we assume that the other ships can't?
|
|
IP Logged |
|
|
|
Archon
Newbie
Gender:
Posts: 39
|
|
Re: Ghost ships
« Reply #5 on: Aug 16th, 2002, 2:56am » |
Quote Modify
|
I have a feeling that captain H doesn't have to do anything, that it is impossible for H to have 3 collisions if both F and G have had 3 collisions. I doubt I have the ability to prove it, but here's a start for someone with more maths ability to pick up.
Certainly, the first step is to turn this problem into one involving lines in 3 dimensions.
Each line will be straight.
The plot of each line is a set of simultaneous equations in x, y and t (t being time)
Let collision between 2 ships (say G and H) occur at xGH, yGH, tGH in this 3d space, and denote the event GH
I hypothesize that there exists no solution for the event EH, where exists:
FE, FG, FH, GE, GH
and where xyt is a different value for each event (because you can clearly draw 4 straight lines in which at least 2 intersect with all other 3 lines if they all pass through the same point)
and where no 2 vectors are the same (the ships hit amidships, so no collision is due to one ship overtaking another on the same vector)
Come to thik of it, this looks like the cigarettes puzzle.
|
| « Last Edit: Aug 16th, 2002, 3:05am by Archon » |
IP Logged |
|
|
|
Archon
Newbie
Gender:
Posts: 39
|
|
Re: Ghost ships
« Reply #6 on: Aug 16th, 2002, 3:11am » |
Quote Modify
|
It is probably also important that both F and G have had 3 collisions *before* the proposed collision between E and H.
|
|
IP Logged |
|
|
|
Archon
Newbie
Gender:
Posts: 39
|
|
Re: Ghost ships
« Reply #7 on: Aug 16th, 2002, 4:05am » |
Quote Modify
|
Hm, some more thought...
Given that, as has been said, in the 3d space the lines must be coplanar, we should be able to transform this back into a 2d problem.
But clearly it is possible to draw 4 lines in 2 dimensions with 2 lines having 3 intersections.
But then time becomes a factor again, because we dont just want 4 intersecting lines, we want them to intersect at specific times. Which takes us back to 3 dimensions... ugh 
|
|
IP Logged |
|
|
|
Chronos
Full Member
Gender:
Posts: 288
|
|
Re: Ghost ships
« Reply #8 on: Aug 17th, 2002, 11:35am » |
Quote Modify
|
Quote:| But then time becomes a factor again, because we dont just want 4 intersecting lines, we want them to intersect at specific times. |
|
That's not actually a problem. No matter how you draw four mutually-intersecting lines on a plane, there are always two lines such that no intersections lie on one side of that line. I don't think I can prove it without a diagram, but you should be able to get it on you own after playing around a bit with lines on a paper. Now, we just pick one of those two lines to be ship H, and tilt it up into the 3-d xyt space in such a way that H is the last collision for E, F, and G. Thus, in the "do nothing" case, H is guaranteed of another collision.
|
|
IP Logged |
|
|
|
pa0pa0
Newbie
Posts: 16
|
|
Re: Ghost ships
« Reply #9 on: Aug 21st, 2002, 5:55am » |
Quote Modify
|
on Aug 5th, 2002, 7:16pm, Paul Hsieh wrote:
The ship captain has many alternatives to get off the plane. One way is to veer off in a purpendicular direction for a short time, then redirect to the target location. This will guarantee leaving the plane, thus missing "E". |
|
I think he has to not only get off the plane, but ensure that he stays off it by either diverging from it or proceeding parallel with it (otherwise he could be terribly unlucky and collide with E at the very moment when he re-intersects the plane).
But he doesn't know the orientation of the plane! In fact, the only thing he knows about the plane (apart from the fact that his current course is on it) is that the plane is *not* parallel with the time-axis (the operative word being "amidships" as noted by Tim). I think this means that his only way of ensuring that he gets and stays off the plane is by changing his speed while *not* changing his direction. i.e zig-zagging doesn't work! He can then either maintain the new speed (diverging from the plane) or resume his old speed (proceeding parallel with the plane.)
Afterthought: if he had measured the speed and direction of G or F when he had the chance, then he could work out the orientation of the plane and get off it by zig-zagging.
|
|
IP Logged |
|
|
|
vijk
Guest
|
I guess that if H simply follows F, no collision with E can occur. But reaching the destination is more difficult.
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
Let's inject this discussion with a diagram.
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Ghost ships
« Reply #12 on: Jul 16th, 2004, 10:55am » |
Quote Modify
|
Here are my thoughts about this problem.
::
As mentionned, without a course change, H is guaranteed to collide with E. Any course change in space (move a bit left) or time (wait a while) will prevent the collision. Unfortunately, it will not guarantee that you will not collide elsewhere. In fact, for every course change for H, there are possible courses for E that still intersect the new course of H. You need to take into account the speed of the other ships to know how to get out of the way.
If H's course change is to stop a while, the problematic courses for E are all the coursese that follow the same path as H, at a different time. But in that case, F and G must also follow that path. So, if the 2 collisions happened by one ship overtaking the other along the same straight path, you can avoid the collision by moving out of that line.
For any other situation, where the ships actually crossed their path at an angle, you know that the last ship is expected to also cross the path at an angle, and at the very time you reach it. In that case, you just need to stop a while or change speed to reach that crossing before or after E reaches it.
::
|
| « Last Edit: Jul 16th, 2004, 10:58am by Grimbal » |
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
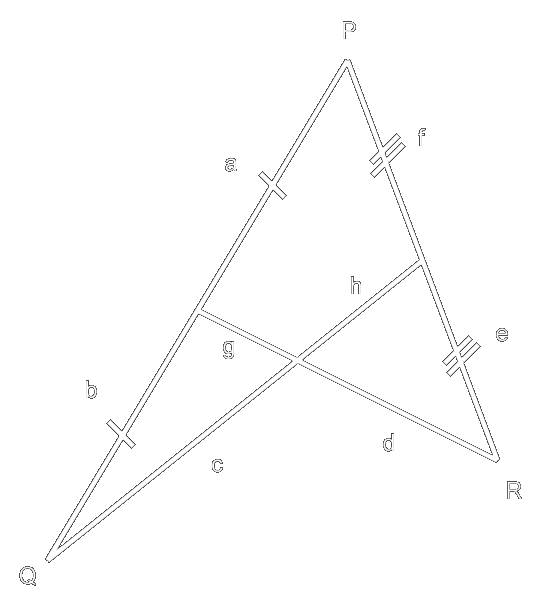
In all there is potential for six collisions - I believe that in order for the first five to occur, the shape formed by the paths of the four ships have to correspond to the diagram given below - in which line segments a and b equal, and c and d are equal. It also turns out that d = 2g and c = 2h. The lengths of these segments directly corresponds to the time it takes for each ship to cover the distances shown. In order for three of the ships to collide as the problem statement describes the path diagram has to look like this. Explanation in subsequent post.
|
| « Last Edit: Jul 16th, 2004, 8:31pm by mattian » |
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Ghost ships
« Reply #14 on: Jul 16th, 2004, 8:56pm » |
Quote Modify
|
Explanation.
Let H be travelling in the direction P to Q
Let G be travelling in the direction R to P
Let F be travelling in the direction R to midpoint PQ
Let E be travelling in the direction Q to midpoint PR
The first collision must occur at R between ships F and G.
The next collision must occur at midpoint PR between E and G while F is at the midpoint of d.
The next collision must occur at intersection of g, h, c, d between E and F ... AND SIMULTANEOUSLY... at P between G and H.
The next collision must occur at midpoint PQ between between F and H while E is at the midpoint of c.
The final collision will absolutely occur at Q between E and H unless H slows down or speeds up. The collision will absolutely not occur between E and H if one of them changes their speed and the ships are of close to zero size.
It is important that they are very small to ensure that small changes in speed correspond to successfully avoiding the collision.
I think the real problem here is that E and H are in the same predicament prior to their collision with each other. And any decision that H makes could be made by E as well which might revive the collision potential.
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Ghost ships
« Reply #15 on: Jul 16th, 2004, 9:05pm » |
Quote Modify
|
Think of the units of time in my explanation as proportional distances travelled or time units which are not necessarily equal from unit to unit but consistent for all ships at a given time. In other words, the first time unit may be 3 minutes while the next is 5 minutes, but this is true for all ships when it applies.
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Ghost ships
« Reply #16 on: Jul 17th, 2004, 3:03am » |
Quote Modify
|
As I mentionned in the post earlier, simply avoiding the expected collision doesn't guarantee that E and H won't collide elsewhere. Changing speed does not work if all ships follow the same path at different speed. They will just collide earlier or later.
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Ghost ships
« Reply #17 on: Jul 17th, 2004, 6:22am » |
Quote Modify
|
By my argument which references the diagram, if any two of them are on the same line, then they're all on the same line. Ship H would know if he were on the same line as F and G when they collided, and would therefore know that E would be on that line too. In that case he could simply branch off from the line and reestablish his original heading parallel to his original course. When E passes him by, he can get back onto his original course, if necessary.
|
|
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
|
Re: Ghost ships
« Reply #18 on: Jul 17th, 2004, 9:03am » |
Quote Modify
|
Lets simplify things right down. Pick the inertial frame of reference in which H is stationary - the other ships will still move at a constant velocity in this new frame.
Since H is stationary in this new frame, G and F must both be moving directly towards H. Since they collide with each other they must be following the same line at different speeds. Unless E is also stationary, or collided with both F and G simultaneously, the two points of collision must be distinct, so E must also be moving on the same line as F and G. If E is approaching H on that line, then collision is inevitable if H does nothing. If E is receding, then the only way collision can occur is if H accelerates towards E.
Back in the original inertial frame of reference, H can avoid collision by accelerating briefly in any direction other than the bearing F and G approached along. If they're not all moving along the same line, then a simple change of speed will suffice, and avoid any navigational complications.
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Ghost ships
« Reply #19 on: Jul 18th, 2004, 10:31am » |
Quote Modify
|
But surely, in the original reference frame in which the ships are moving with respect to a stationary ocean, H's brief impulse accelaration should be in a direction which differs from the directions of all three of the other ships (E, F and G) and not just those with which H has already collided (F and G). If that is true, then how will H know E's vector in order to avoid this?
|
|
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2873
|
|
Re: Ghost ships
« Reply #20 on: Jul 19th, 2004, 4:07am » |
Quote Modify
|
But in the original ocean-stationary frame, the line along which the ships are moving in the H-stationary frame is moving at a constant speed, and at any point in time, all four ships are on it. If you resolve vectors into horizontal components parallel to that line and perpendicular to it, then any acceleration parallel to the line will keep H on the line and potentially headed for a collision, while acceleration in any other direction will have a non-zero component non-parallel to the line, so will move H off the line.
As to the problem of other ships also changing their motion, only H has been in two third collisions, so only H knows that E and H are on a collision course, so H is the only ship with a reason to take evasive maneuvers.
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Ghost ships
« Reply #21 on: Jul 19th, 2004, 5:26am » |
Quote Modify
|
I'm still working on understanding your first statement - I am resigned now to the fact that I'm a bit slower than you and it takes me a little while to catch up.
Re: Your second statement; I follow you. Though E, like H, has in fact had two collisions, E did not hear the other captains say, "that's our third collision". Agreed.
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: Ghost ships
« Reply #22 on: Jul 21st, 2004, 12:50pm » |
Quote Modify
|
RMS is absolutely right. H has to get off the straight line formed by the ships E, F, G and H in the reference frame in which H is stationary. In the standard reference frame - i.e. such that the ocean is stationery - E is either always directly ahead of H or never directly ahead of H. If E is directly ahead of H, H simply needs to move over a little bit. If E is not directly ahead of H, H simply needs to accelerate or decelerate briefly. H will know that E is directly ahead, if its collisions with F and G were directly head on.
|
| « Last Edit: Jul 21st, 2004, 12:52pm by mattian » |
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2873
|
|
Re: Ghost ships
« Reply #23 on: Jul 23rd, 2004, 3:48am » |
Quote Modify
|
Actually, E could also be directly behind throughout - in which case the other two ships will have overtaken H, with G moving faster than F moving faster than E, in which case H could just accelerate to match F's speed in which case E can never catch up. If E is ahead, then the only way to avoid collision and still reach the original destination is to move to one side, and do whatever recalculations are necessary (and hope the collision doesn't happen anyway at the destination...)
|
|
IP Logged |
|
|
|
jonderry
Newbie
Posts: 18
|
|
Re: Ghost ships
« Reply #24 on: Aug 17th, 2004, 10:17am » |
Quote Modify
|
It is true that the ships all move along one line in the inertial frame of H, but I believe it is impossible for H's captain to compute the direction of that straight line; the line could point anywhere in 3D area-time.
Unless I am missing something, the only surefire solution appears to be making the earlier assumption that the ships are not moving in the same direction in space at different speeds (from the fact that the collisions are amidships), so that slowing down and speeding back up again in the same direction takes you off of the common plane.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print
Remove