Author |
Topic: Power set of natural numbers (Read 3810 times) |
|
Rajan
Newbie
Gender: 
Posts: 5
|
 |
Power set of natural numbers
« on: Mar 31st, 2010, 1:21am » |
 Quote  Modify
|
For any set A, Cantor's theorem states that the Power set of A cannot be 1-1 with A and is also proved for countably infinite sized A.
However, I devised a construction which tries to achieve this bijection for a countably infinite set. Since it is opposite to an established theorem, there might be a flaw (or not). Can you spot a flaw? Here is the construction...
The power set of whole numbers consists of
0. {}
1. {0}, {1}, {2}, {3},...
2. {0,0}, {0,1}, {1,0}, {1,1}, {0,2},...
3. {1,1,1},{1,1,2},...
... ...
List 0 is of finite size.
We know that there are countably infinite sets in List 1.
Lemma: List 2 is also countably infinite in size. To show this, we can imagine the set {a,b} as the integral grid point (a,b) in 2d space. Each grid point in the first quadrant of this 2-d plane maps to a unique set in list 2. Now the final step - to map whole numbers to each grid point, we can map 0 to the origin and move in a zig zag pattern (see zigzag pattern image below). This pattern maps a whole number to each set in List 2.
Lemma : List 3, 4 and onwards can also be proved to be countably infinite with a similar construction. I am not proving this as the construction seems intuitively similar. (this is one possible flaw, as I have not proved that this can be carried out for every List, but I feel this to be intuitively correct)
Now we have a countably infinite sequence of lists, each of which contains countably infinite sets. We can assign each of these sets to a 2d grid point in the following manner...
For list 1 - {0} maps to {1,0},
{1} maps to {1,1},
{k} maps to {1,k}...
For list 2 - {0,0} maps to {2,0},
{1,0} maps to {2,1},
{0,1} maps to {2,2},
{m,n} maps to {2,p}...
For list 3 - {0,0,0} maps to {3,0},
{1,0,0} maps to {3,1},
{0,1,0} maps to {3,2},
{m,n,k} maps to {3,t}...
and so on...
All these points are on the countably infinite grid points of the 1st quadrant of the 2d plane. We can simply map them to the whole numbers again using the same zigzag trick we used earlier for List 2.
This way, each subset of the power set, no matter its elements (as long as all its elements are finite), can be mapped to a unique finite whole number. QED.
I am sure this is the kind of thing every set theory student goes through in their coursework... I am new to it and cant see the flaw readily (or maybe there is none  ).
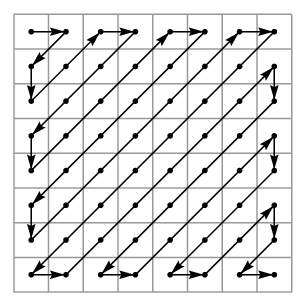
The zigzag shown here is constrained in a 8x8 square. In a 2d plane with 2 sides open, the zigzags continue to get larger and larger.
|
| « Last Edit: Mar 31st, 2010, 1:42am by Rajan » |
 IP Logged |
|
|
|
pex
Uberpuzzler
Gender:
Posts: 880
|
|
Re: Power set of natural numbers
« Reply #1 on: Mar 31st, 2010, 1:53am » |
Quote Modify
|
Your construction works fine for finite-sized subsets; however, what will you do with the infinite-sized ones? Specifically, in your construction, where does the complete set of whole numbers go?
|
|
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
|
Re: Power set of natural numbers
« Reply #2 on: Mar 31st, 2010, 8:20am » |
Quote Modify
|
Another minor quibble: {1,1} isn't a subset of the natural numbers - or at least not a different subset from {1}. Also {0,1} and {1,0} are not distinct sets.
Neither of those objections invalidates the original argument - the problem, as pex pointed out, is that the construction only covers the finite subsets. You can use a similar construction to cover the co-finite subsets (those whose complements are finite) but there's still a vast (uncountable by Cantor's theorem) number of infinite subsets whose complements are also infinite which you have to take account of somehow...
|
|
IP Logged |
|
|
|
pex
Uberpuzzler
Gender:
Posts: 880
|
|
Re: Power set of natural numbers
« Reply #3 on: Mar 31st, 2010, 8:29am » |
Quote Modify
|
Actually, there is a much simpler construction that achieves exactly the same result as yours: just sort each subset {x1, x2, x3, ..., xn} so that
x1 < x2 < x3 < ... < xn
and assign to it the natural number
(2^x1)*(3^x2)*(5^x3)*...*(pn^xn).
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Power set of natural numbers
« Reply #4 on: Mar 31st, 2010, 8:33am » |
Quote Modify
|
Or 2x1 + 2x2 + 2x3 + ... + 2xn
|
| « Last Edit: Mar 31st, 2010, 8:35am by Grimbal » |
IP Logged |
|
|
|
pex
Uberpuzzler
Gender:
Posts: 880
|
|
Re: Power set of natural numbers
« Reply #5 on: Mar 31st, 2010, 8:41am » |
Quote Modify
|
on Mar 31st, 2010, 8:33am, Grimbal wrote:| Or 2x1 + 2x2 + 2x3 + ... + 2xn |
|
Yeah, that's a lot more economical.
|
|
IP Logged |
|
|
|
Rajan
Newbie
Gender:
Posts: 5
|
|
Re: Power set of natural numbers
« Reply #6 on: Mar 31st, 2010, 10:15am » |
Quote Modify
|
Thanks for the responses... Pex's and Grimbal's construction were beautiful.
rmsgrey - that gives me some food for thought. This stuff borders on crazy... my mind start to numb after a few minutes of thought. No wonder Mathematicians were extremely touchy about it.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print