Author |
Topic: what is google calculator doing? (Read 939 times) |
|
Benny
Uberpuzzler
Gender: 
Posts: 1024
|
 |
what is google calculator doing?
« on: Jul 24th, 2009, 11:32am » |
 Quote  Modify
|
What I know is we cannot use the factorial function onto non-whole, negative or complex numbers.
Google calculator gave me this:
4 ! = 24
5 ! = 120
4.5 ! = 52.3427778
4.85 ! = 93.0961354
(-3.5) ! = -0.94530872
(-4.5) ! = 0.270088206
(2 + (4 * i)) ! = 0.00522553847 - 0.172547079 i
What are these? What is google calculator doing?
I read that some mathematicians decided they wanted to interpolate the factorial function to find "what values would be" between the integers... and "extrapolate" for negatives as well.
They found that there are several functions that can do that but these functions do not always agree at the exact values for interpolated and extrapolated inputs.
The most popular function is the Gamma Function
Is the gamma function the proper function to extrapolate negative whole numbers but not the proper function to interpolate non-integers?
|
| « Last Edit: Jul 24th, 2009, 11:33am by Benny » |
 IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: what is google calculator doing?
« Reply #1 on: Jul 24th, 2009, 4:21pm » |
Quote Modify
|
Google calculator is writing
x! = Gamma(x+1)
and using this for calculating non-integer values. The gamma function satisfies the recurrence relation Gamma(x+1) = x * Gamma(x), which is reminiscent of the factorial's recurrence relation. This, however, is not enough to specify what Gamma is. We would like the extension of factorial to be what is called "analytic," though, which basically means the function is given by a power series (locally, anyways). Unfortunately, this still doesn't specify what Gamma has to be. You can further require Gamma to be logarithmically convex, and that will be enough to specify Gamma uniquely.
For negative integer values, Gamma has a pole (i.e. it is infinite). Interestingly, google calculator doesn't like (-3)!, and does a google search instead.
In many senses, Gamma is the best way to interpolate other values of the factorial. However, I wouldn't go so far as to say 4.5! = 52.34...; I would merely say that a reasonable interpretation of 4.5! is Gamma(5.5), which equals 52.34....
|
| « Last Edit: Jul 24th, 2009, 4:22pm by Obob » |
IP Logged |
|
|
|
Benny
Uberpuzzler
Gender:
Posts: 1024
|
|
Re: what is google calculator doing?
« Reply #2 on: Jul 24th, 2009, 5:02pm » |
Quote Modify
|
Okay. So,
gamma(n+1) = n! for non-negative n
How do you define (1/2)! ?
(I'm getting a weird result)
|
| « Last Edit: Jul 24th, 2009, 5:13pm by Benny » |
IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: what is google calculator doing?
« Reply #3 on: Jul 24th, 2009, 5:25pm » |
Quote Modify
|
For z with positive real part, Gamma(z) =  0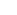 tz-1e-t dt, and (1/2)! should be interrpreted as Gamma(3/2). The integral evaluates to  ( )/ 2.
|
| « Last Edit: Jul 24th, 2009, 5:27pm by Obob » |
IP Logged |
|
|
|
Benny
Uberpuzzler
Gender:
Posts: 1024
|
|
Re: what is google calculator doing?
« Reply #4 on: Jul 24th, 2009, 11:07pm » |
Quote Modify
|
on Jul 24th, 2009, 5:25pm, Obob wrote:| For z with positive real part, Gamma(z) = 0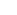 tz-1e-t dt, and (1/2)! should be interrpreted as Gamma(3/2). The integral evaluates to ()/ 2. |
|
Thanks, Obob .... It's clear now ... I should have checked my calculus book.
This wiki document discusses, too, and in particular
(n + 1/2)! =
and, The Gamma function is in fact defined for all complex numbers z except for the nonpositive integers
|
|
IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: what is google calculator doing?
« Reply #5 on: Jul 25th, 2009, 1:09pm » |
Quote Modify
|
Gamma is defined for all complex numbers except the nonpositive integers. However, the formula I gave is not the correct definition if z has negative real part; the integral doesn't converge then. For negative z, Gamma is defined by analytic continuation.
Here's another definition of Gamma which is valid for all z where it is defined:
Gamma(z) = limit as n->infty of n! nz/(z(z+1)(z+2)...(z+n)).
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print