 Author
Author |
Topic: The Real Projective Line (Read 1282 times) |
|
Sir Col
Uberpuzzler
    

impudens simia et macrologus profundus fabulae

Gender: 
Posts: 1825
|
 |
The Real Projective Line
« on: Sep 23rd, 2007, 9:37am » |
 Quote Quote  Modify Modify
|
Does anyone know much about the real projective line extension of the real number system?
http://en.wikipedia.org/wiki/Real_projective_line
I'm particularly interested in the "definition", a/0 = inf, where a is non-zero and belongs to the set of reals.
In which case, wouldn't inf*0 be undefined? (It could be equal to any real quantity.)
However, as inf*a = inf, then multiplying any non-zero real by infinity is properly defined. Hence it is multiplying by zero that becomes the new "undefined". It seems that they're just replacing one undefined calculation: a/0, with another: 0*inf.
In fact, is a*0 properly defined?
|
|
 IP Logged IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: The Real Projective Line
« Reply #1 on: Sep 23rd, 2007, 10:25am » |
 Quote Quote  Modify Modify
|
on Sep 23rd, 2007, 9:37am, Sir Col wrote:I think Icarus explained it somewhere once.
Quote: I'm particularly interested in the "definition", a/0 = inf, where a is non-zero and belongs to the set of reals.
In which case, wouldn't inf*0 be undefined? (It could be equal to any real quantity.) |
|
According to that wiki-page it is undefined.
Quote:| However, as inf*a = inf, then multiplying any non-zero real by infinity is properly defined. Hence it is multiplying by zero that becomes the new "undefined". It seems that they're just replacing one undefined calculation: a/0, with another: 0*inf. |
|
Both are undefined normally, so I don't see how it's a replacement.
Actually, 0*inf isn't even a valid expression in normal arithmetic, because inf isn't a number there.
Quote:| In fact, is a*0 properly defined? |
|
If a is not infinity, sure.
|
| « Last Edit: Sep 23rd, 2007, 10:27am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Sir Col
Uberpuzzler
    

impudens simia et macrologus profundus fabulae

Gender: 
Posts: 1825
|
 |
Re: The Real Projective Line
« Reply #2 on: Sep 23rd, 2007, 12:17pm » |
 Quote Quote  Modify Modify
|
on Sep 23rd, 2007, 10:25am, towr wrote:| Actually, 0*inf isn't even a valid expression in normal arithmetic, because inf isn't a number there. |
|
Duh! I don't know what I was thinking. 
Which reminds me of three interesting "arguments"...
(i) inf * 0 = 0 + 0 + 0 + ... = 0
(ii) As y tends towards infinity x/y tends towards zero. Therefore x / inf = 0. Hence inf * 0 = x; that is, any finite value you want.
(iii) Consider the algebraic identity, x * 1/x = 1, which is defined for finite x. As x tends towards infinity, 1/x tends towards zero, so the limit of x * 1/x = inf * 0 = 1.
|
|
 IP Logged IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
Sir Col
Uberpuzzler
    

impudens simia et macrologus profundus fabulae

Gender: 
Posts: 1825
|
 |
Re: The Real Projective Line
« Reply #3 on: Sep 23rd, 2007, 12:24pm » |
 Quote Quote  Modify Modify
|
And whilst I'm at it I may as well post another old favourite...
As x / y = 1, it follows that inf / inf = 1.
Therefore (inf + inf) / inf = inf / inf = 1
And (inf + inf) / inf = inf / inf + inf / inf = 1 + 1 = 2.
Hence 1 = 2. 
|
|
 IP Logged IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: The Real Projective Line
« Reply #4 on: Sep 23rd, 2007, 12:28pm » |
 Quote Quote  Modify Modify
|
How about:
inf = card(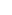 ) )
0 =card(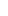 ) )
inf * 0 = card(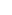 x x 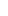 ) = card( ) = card(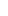 ) = 0 ) = 0
And of course with these kinds of zeros and this kind of multiplication, unless I'm missing something, 0*a=0 for all a (even if a is infinite).
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: The Real Projective Line
« Reply #5 on: Sep 23rd, 2007, 3:01pm » |
 Quote Quote  Modify Modify
|
Well we do want to be able to do arithmetic with more than just integers, so defining multiplication in terms of cardinalities can't be done in general.
Really, though, either you can define a/0=inf or inf.0=0 without having any serious arithmetic issues. Once you define both, the arithmetic no longer behaves as nicely as you want it to.
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: The Real Projective Line
« Reply #6 on: Sep 26th, 2007, 12:23am » |
 Quote Quote  Modify Modify
|
I like the geometrical apsect of this. Consider the following statement from Euclidian geometry:
Two lines intersect in exactly one point except when they are parallel.
In projective geometry (where lines are projective) the "except" part can be removed!
This is also true for some nice transformations (like inversion or reciprocation w.r.t. circle).
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: The Real Projective Line
« Reply #7 on: Sep 26th, 2007, 9:01am » |
 Quote Quote  Modify Modify
|
on Sep 26th, 2007, 12:23am, Barukh wrote:I like the geometrical apsect of this. Consider the following statement from Euclidian geometry:
Two lines intersect in exactly one point except when they are parallel.
In projective geometry (where lines are projective) the "except" part can be removed!
|
|
This is new to me. So does this mean, in projective geometry, the parabola y=x2 and the line y=x have two points of intersection?
Edit: oops I meant 3. (0,0), (1,1), ( , ,  ) )
|
| « Last Edit: Sep 26th, 2007, 9:20am by Sameer » |
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: The Real Projective Line
« Reply #8 on: Sep 26th, 2007, 9:16am » |
 Quote Quote  Modify Modify
|
yes
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register