 Author
Author |
Topic: 3D Objects described by equations (Read 810 times) |
|
Drizzle_of_Spirits
Newbie


Posts: 6
|
 |
3D Objects described by equations
« on: Mar 6th, 2007, 7:31am » |
 Quote Quote  Modify Modify
|
( I don't know where to place this problem. Is it appropriate to be placed in this hard section??
I give permission to Wu, Icarus or Towr to move it  ) )
I remember the time when I took my calculus class. I was really excited to know that by using equations, we could describe many 3D objects.
For example:
x2+y2+z2=C
can be used to describe a sphere with various values of diameter.
A question then appeared in my mind and I asked my lecturer:
"How about our earth? Do we already have a set of equations that EXACTLY describes the earth?"
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: 3D Objects described by equations
« Reply #1 on: Mar 6th, 2007, 8:37am » |
 Quote Quote  Modify Modify
|
Not 'exactly'. But the Earth is nearer to an oblate spheroid than a perfect sphere.
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: 3D Objects described by equations
« Reply #2 on: Mar 6th, 2007, 8:39am » |
 Quote Quote  Modify Modify
|
on Mar 6th, 2007, 7:31am, Drizzle_of_Spirits wrote:| "How about our earth? Do we already have a set of equations that EXACTLY describes the earth?" |
|
"EXACTLY" is unfortunately impossible since it continuously changes and we can't at the same time know both position and velocity of each particle exactly.
It's pretty much a sphere though, upto a fraction of a percent
Quote:| The diameter from the North Pole to the South Pole (the shortest diameter) is approximately 12,714 km. The equatorial diameter (the longest diameter) is approximately 12,756 km. |
|
And if you take a momentary snapshot, you could fit a function through all surface points. The more you neglect, like mountains and valleys, the easier a description becomes.
|
| « Last Edit: Mar 6th, 2007, 8:43am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 3D Objects described by equations
« Reply #3 on: Mar 6th, 2007, 3:47pm » |
 Quote Quote  Modify Modify
|
on Mar 6th, 2007, 7:31am, Drizzle_of_Spirits wrote:( I don't know where to place this problem. Is it appropriate to be placed in this hard section??
I give permission to Wu, Icarus or Towr to move it  ) ) |
|
Thank you for giving us permission (though of course, you wouldn't be able to prevent it).
Since this isn't a riddle or puzzle, but rather a discussion, I've moved it to the general forum.
-------------------------------------
The first problem with exactly describing the Earth mathematically is that you need to exactly define what you mean by "the Earth". Sure, you can say "this planet we live on", but what exactly are you consider to be part of the planet, and what is not? Do you consider the air to be part of the planet, or just the solid & liquid parts? If you include the air, how far out do you put the boundary between gas particles that are part of Earth and those that are not? If not, then what about plants, animals, people, buildings, etc? Are they to be included or not? Either way you decide that causes problems. Even if we ignore that, there is the question of where exactly the solid/liquid vs air boundary lays. There is a continual exchange of atoms between solids & liquids and the atmosphere that surrounds them.
The fact is, the definition of any physical object is "fuzzy" when examined closely. You can only describe something to at best the accuracy with which it is defined.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Drizzle_of_Spirits
Newbie


Posts: 6
|
 |
Re: 3D Objects described by equations
« Reply #4 on: Mar 8th, 2007, 12:04am » |
 Quote Quote  Modify Modify
|
To simplify, say that we consider only the solid/liquid parts, ignoring the exchange of materials, velocity and changes.
In other words, to be simpler, imagine a perfect sphere with some parts (as mountains,etc); can we describe that 3D Object with some simple equations? Or do we need any advanced mathematical tools to describe it?
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 3D Objects described by equations
« Reply #5 on: Mar 8th, 2007, 4:30pm » |
 Quote Quote  Modify Modify
|
Advanced mathematical tools. You can model it to any proscribed accuracy by equations, but the closer you want your model to get to the actual shape, the more equations and parameters you need. The more complex the shape is, the more complex the model has to be.
This is actually provable. Every shape has a certain content of information. Every mathematical model does as well. The more complex either is, the more information it contains. In order to accurately represent the shape, the model must contain as much information as the shape does. By lowering the accuracy of our representation, we can get away with a less complex model, as we only need to represent the least complex shape that differs from the actual shape by an acceptable margin. But the closer we require the model to be to the real thing, the more information it must contain.
For example: A perfect sphere contains very little information: it is completely determined 4 parameters: it's center (x, y, z) and its radius. Likewise, the equation that represents it also depends on just 4 parameters.
Now let's put an "infinitesimal bump" on our sphere: a single point whose location must be matched by a special point in the model. This introduces 2 more parameters independent of the others, to specify where on the sphere this point is. If I add more special points, I require 2 more parameters for each of them. Any equation or set of equations I use to model my pointed sphere has to have at least as many free parameters to be able to represent the sphere with complete accuracy. But next, consider what happens when the bump is no longer infinitesimal. Now I also need more parameters to specify the shape. At the very least this will require an additional 2 parameters (for a smaller spherical bump on the main sphere). The more complex the shape of the bump is, the more parameters are needed.
Now look at the earth. What rules there are that control where topological feature are located relative to each other are very loose. Effectively, each mountain, hill, valley, knoll, depression, is a shaped bump, whose characteristics are independent of those around it. (This may seem to overstate matters since, for example, high mountains tend accompany other high mountains. But even a tiny amount of freedom in each mountain's height contains the same informational content as a deep valley would in the same place.) To represent the earth to "perfect accuracy" (assuming you overcome the obstacles I pointed out in my earlier post and come up with a suitably well-defined concept of what Earth is) would require billions upon trillions upon quadrillions of independent parameters.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: 3D Objects described by equations
« Reply #6 on: Mar 9th, 2007, 4:58am » |
 Quote Quote  Modify Modify
|
Considering that the shape of Earth is mostly determined by gravity, could we compute the shape of a ball of liquid, considering just gravity and the centrifugal force due to the rotation?
To be precise, the force and direction of gravity at the surface depends on the shape of the ball. So I bet it is not solvable exactly. But maybe the gravity field is close enough to that of a spherical ball?
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: 3D Objects described by equations
« Reply #7 on: Mar 9th, 2007, 7:56am » |
 Quote Quote  Modify Modify
|
on Mar 9th, 2007, 4:58am, Grimbal wrote:Considering that the shape of Earth is mostly determined by gravity, could we compute the shape of a ball of liquid, considering just gravity and the centrifugal force due to the rotation?
|
|
Assuming a fluid planet of uniform density, Wikpedia gives
Flattening = (a-b)/a = 1 - b:a 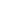 3 3 /2G /2G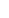 T2 T2
where
a = equitorial radius
b = polar radius
G = gravitational constant
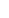 = density = density
T = rotation period
|
| « Last Edit: Mar 11th, 2007, 5:27pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
SWF
Uberpuzzler
    

Posts: 879
|
 |
Re: 3D Objects described by equations
« Reply #8 on: Mar 11th, 2007, 5:03pm » |
 Quote Quote  Modify Modify
|
While still a long way from exactly describing the earth's surface, using the assumptions Grimbal suggests for a liquid planet, the equation I come up with for shape of an incompressible liquid planet is an ellipsoid of revolution:
P = d*(x2 + y2) + c*z2
where
P=pressure at center of planet
c= 2*pi*(rho)2G/3
d= c- 2*pi2*(rho)/T2
rho, T, and G are as defined by Thudanblunder, and the flattening parameter would equal sqrt(1-3*pi/(G*rho*T2), which for large rho*T is close to the Wikipedia approximation.
|
| « Last Edit: Mar 16th, 2007, 6:33pm by SWF » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register