Author |
Topic: Geometric puzzle, two triangles (Read 385 times) |
|
rmsgrey
Uberpuzzler
    
Gender: 
Posts: 2874
|
 |
Geometric puzzle, two triangles
« on: Dec 19th, 2023, 9:49am » |
 Quote  Modify
|
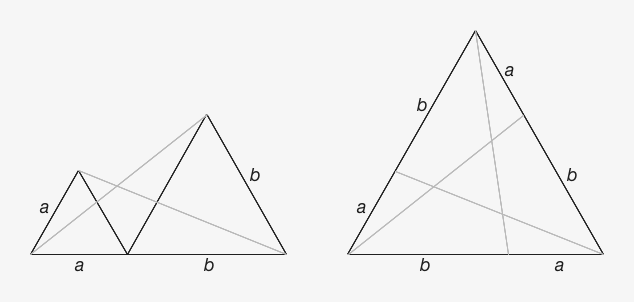
Take a horizontal line segment and mark any point on it to divide it into two segments. For each of those two segments, construct an equilateral triangle with that segment as one side, and the third corner above the line (so both triangles are on the same side).
For each triangle, draw the line connecting its apex to the opposite end of the baseline. Those two lines cross.
What is the angle above those two lines where they cross?
|
|
 IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
If you put these lines in the proper perspective the answer becomes almost obvious.
|
| « Last Edit: Feb 17th, 2024, 7:07am by Grimbal » |
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
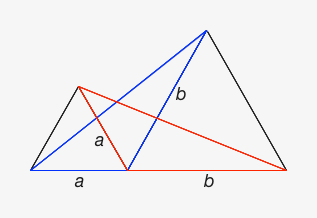
Now that I think of it, The blue triangle and the red triangle below are the same, just rotated 60°.
Now the problem is that my first answer would imply an angle of 120° (1/3 of 360°). The second answer says it is 60°. So which one is it? And where did I go wrong?
|
| « Last Edit: Feb 17th, 2024, 10:13am by Grimbal » |
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2874
|
|
Re: Geometric puzzle, two triangles
« Reply #3 on: Feb 18th, 2024, 5:55am » |
Quote Modify
|
on Feb 17th, 2024, 10:13am, Grimbal wrote:Now that I think of it, The blue triangle and the red triangle below are the same, just rotated 60°.
Now the problem is that my first answer would imply an angle of 120° (1/3 of 360°). The second answer says it is 60°. So which one is it? And where did I go wrong? |
|
This is the proof I came up with.
The 60 degrees is the angle to the side of the intersection (the space you rotated the line through), which makes the angle above the intersection 180-60=120.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
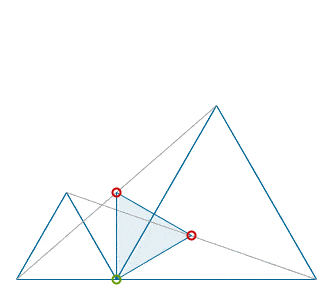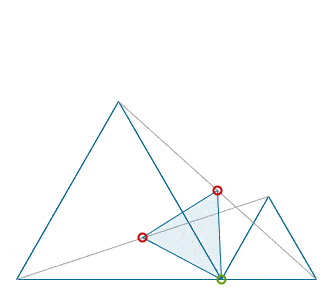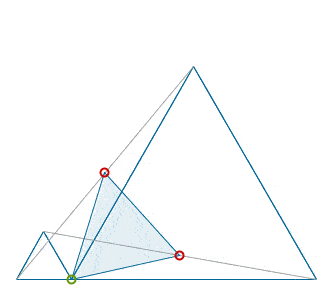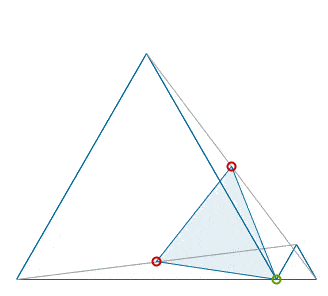
Nice catch, rmsgrey. There is one more nontrivial equilateral triangle lurking in your find: if the dead middles of the cross lines are marked (in red) then under the rotation of the parent plane about the (green) dividing point, counter or clockwise, by sixty degrees, one of these red points will be taken into the other and, as such, the corresponding triangle constructed on the green dividing point and the two red mid points must be equilateral as well.
I tried to capture this in the animation below.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
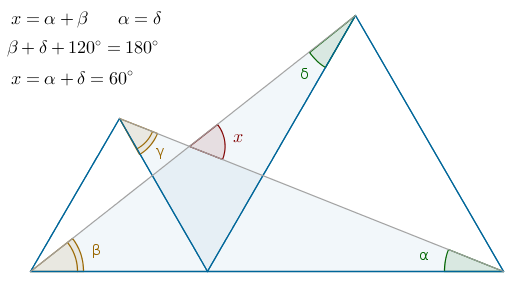
As far as the original problem goes, since you guys already picked an elegant way to solve it, the simple angle chasing does it.
The magnitude of the angle sought-after, x, is the exterior angle of the corresponding triangle and, as such, is equal to the sum of the magnitudes of the two opposite interior angles.
But the two triangles shown in solid blue are congruent by SAS, from where the solution follows: the angle above the crossing lines is 120 degrees.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
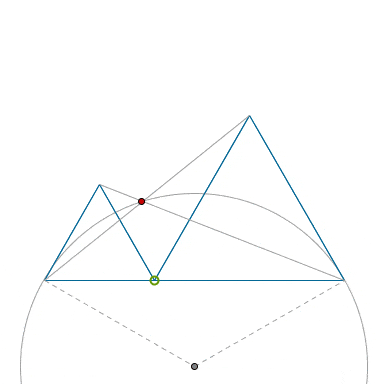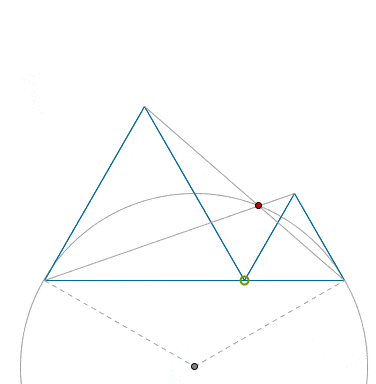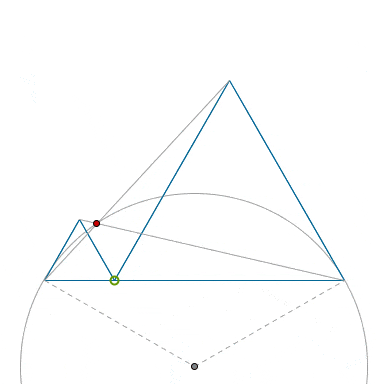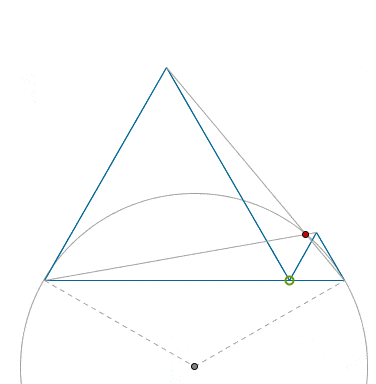
That, clearly, means that that trajectory of the crossing point, shown in red, belongs to a (smaller) circular arc, as a I tried to capture that fact in the animation below.
The center of the said circle is located trivially: just construct the perpendiculars to the sides of the given equilateral triangles, etc.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print