Author |
Topic: Snail Trail (Read 1240 times) |
|
rloginunix
Uberpuzzler
Posts: 1029
|
Snail Trail
Apologies if my drawing skills are not up to snuff but the sketch below is supposed to depict a right square prism made of glass with its dimensions shown:
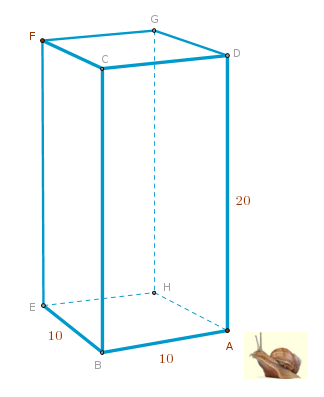
1). What is the shortest trail the snail can trail from the point A to the point F?
2). To which point on the surface of the prism will the snail trail the longest?
|
|
 IP Logged |
|
|
|
alien2
Uberpuzzler
Gender: 
Posts: 6991
|
 |
Re: Snail Trail
« Reply #1 on: May 8th, 2015, 2:00am » |
 Quote  Modify
|
1. The shortest trail is a straight line if the snail moves on my LCD screen.
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Snail Trail
« Reply #2 on: May 8th, 2015, 5:53am » |
Quote Modify
|
1) There are essentially two possible path to consider for the shortest route: from point A, cross edge BC at its midpoint then continue to point F or from point A, cross edge CD 1/3 of the way from point C then continue to point F. All other potentially-shortest paths are reflections or reversals of these two. By looking at the mesh of the prism, we find that the first way has length  (202 + (10 + 10)2) = 202, while the second way has length (102 + (10 + 20)2) = 1010 which is slightly longer, thus the first route is the shortest possible.
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Snail Trail
« Reply #3 on: May 8th, 2015, 7:53am » |
Quote Modify
|
Alien's statement contains a key to solving this problem but before it can be employed a certain transformation must be applied to the prism - an observation picked up by SMQ - you are correct on number one, 202 is it.
A hint for number two: SMQ's analysis of number one.
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Snail Trail
« Reply #4 on: May 8th, 2015, 8:50am » |
Quote Modify
|
2) First, a sanity check: by arranging meshes on top of one another and plotting the arcs at 202 from each point A (http://dwarfrune.com/smq/wu/SnailTrailMesh1.png), we see that there is indeed a small area of points (a dart-shaped region to near point F) farther away from point A than point F is, no matter the chosen path.
Next, to find the furthest path, we assign a coordinate system: let point F be at (0,0). From symmetry we know that the furthest point must lie on segment FD and be equidistant from all projections of point A (http://dwarfrune.com/smq/wu/SnailTrailMesh2.png). Thus we're searching for a point (x,x) such that ((20 + x)2 + (20 - x)2) = ((10 - x)2 + (30 - x)2). Squaring both sides, and simplifying gives 80x = 200  x = 5/2 = 2.5.
Thus the point on the prism farthest from point A is 1/4 of the way along segment FD from point F.
--SMQ
edit: fixed bad image URL
|
| « Last Edit: May 8th, 2015, 8:53am by SMQ » |
IP Logged |
--SMQ
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Snail Trail
« Reply #5 on: May 8th, 2015, 6:43pm » |
Quote Modify
|
A beautiful solution beautifully arranged. Nothing to add, nothing to take away.
One thing if you do not mind - I use GeoGebra for the geometric constructions. What is your choice? Thanks in advance.
|
|
IP Logged |
|
|
|
pex
Uberpuzzler
Gender:
Posts: 880
|
|
Re: Snail Trail
« Reply #6 on: May 8th, 2015, 8:40pm » |
Quote Modify
|
If I may add:
3). Which two points are furthest from each other using this metric?
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Snail Trail
« Reply #7 on: May 9th, 2015, 3:45am » |
Quote Modify
|
@rloginunix: I've never gotten around to installing dedicated geometry software, so I generally use whatever is handy. Usually either MS Word, as above, or if programming is already involved, FreeBasic which is still my goto language for get-pixels-on-the-screen type problems. 
@pex: my first hypothesis is the centers of the square faces which are 30 units apart, but I haven't attempted a formal analysis yet.
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
pex
Uberpuzzler
Gender:
Posts: 880
|
|
Re: Snail Trail
« Reply #8 on: May 9th, 2015, 4:14am » |
Quote Modify
|
on May 9th, 2015, 3:45am, SMQ wrote:| my first hypothesis is the centers of the square faces which are 30 units apart, but I haven't attempted a formal analysis yet. |
|
That was what my intuition told me too - but it appears that this is not the case!
I haven't attempted a complete formal analysis either, but I have found two points that are slightly further apart, satisfy a similar sort of optimality condition as in your analysis of problem 2, and are not improved upon by some quick numerical optimization attempts.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Snail Trail
« Reply #9 on: May 9th, 2015, 11:26am » |
Quote Modify
|
Awesome minimax idea, pex - two snails! At which points on the surface of the prism must two snails be placed so that they trail towards each other the longest? Let's do it.
There are two basically different paths from A to F: via one or two faces. A path via one face was tested and eliminated in 1) but here in 3) we have to consider it:
A bird's eye view of all the one-face trails
(the drawing came out too big so I truncated its top portion but you get the idea)
The analysis of 1) and 2) tells us that the two points sought-after should be placed somewhere on the bottom and top faces of the prism. Let us assume that a point on the ABEH (bottom) face is X with coordinates (a, b) counting from A (a along AB, b along AH) and that a point on the DCFG (top) face is Y with coordinates (c, d) counting from F (c along FG, d along FC). Let us then put down the lengths of all the possible paths:
P21 = (10 - a - c)2 + (30 + b - d)2
P22 = (10 - b - d)2 + (30 - a + c)2
P23 = (10 - a - c)2 + (30 - b + d)2
P24 = (10 - b - d)2 + (30 - a + c)2
We see that the paths P1 and P3 have the first terms identical. Omitting the squares, their second terms however differ by 2*(b - d). Therefore the lengths of these two paths differ the more b and d differ where one variable grows while the other one diminishes. However, we want to find such values of these variables when all the paths are long enough. So if we assume that b and d are different we can replace them with their half-sum (b + d)/2 in which case the smaller of P1 and P3 will grow and the larger will diminish but P2 and P4 will remain the same - their terms that depend on b and d are the same. Therefore we can take it that b == d and P1 == P3.
By similar reasoning we can take it that a == c and P2 == P4.
Now let us compare P1 and P2. For which b and a, say, P1 < P2:
P21,3(b=d, a=c) = (10 - 2a)2 + 302
P22,4(b=d, a=c) = (10 - 2b)2 + 302
(10 - 2a)2 + 302 < (10 - 2b)2 + 302
a > b
Therefore it is equally long to trail from X to Y if a == b which means that X and Y should be placed on the diagonals of their faces. In that case the length of the path via one face is:
P2(one-face) = (10 - 2a)2 + 302 = 4a2 - 40a + 1000
a horns up parabola. Its first derivative is 8a - 40 so its minimum is at a = 5. Which means that the farther X an Y from the centers of their faces or the closer X and Y to A and F respectively - the longer the corresponding trail.
What remains to do next is to analyze the two-face trail. Derive the length of its path and compare it to the one above.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Snail Trail
« Reply #10 on: May 9th, 2015, 11:51am » |
Quote Modify
|
Since SMQ did all this nice work let me shamelessly, khm, borrow it - from SMQ's last drawing we quickly conclude that the length of the two-face diagonal to diagonal path is:
P2(two-face) = (20 - 2x)2 + (20 + 2x)2
Equating the lengths of two paths we get (setting a = x in my one-face formula):
8x2 + 800 = 4x2 - 40x + 1000
4x2 + 40x - 200 = 0
x2 + 10x - 50 = 0
x = 5((3) - 1)
Therefore the square of the length of this path is:
400(4 - (3))
I went a bit too fast, may be I erred somewhere but that's the number I get.
|
|
IP Logged |
|
|
|
pex
Uberpuzzler
Gender:
Posts: 880
|
on May 9th, 2015, 11:51am, rloginunix wrote:Therefore the square of the length of this path is 400(4 - (3))
I went a bit too fast, may be I erred somewhere but that's the number I get. |
|
Well done - at least, I get the same number. Please see the attachment for a drawing of all six paths of equal length.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Snail Trail
« Reply #12 on: May 10th, 2015, 9:30am » |
Quote Modify
|
Then I think it must be it. On their respective faces the two points sought-after are situated on the diagonals and are symmetrical about the center of the cuboid. They are offset from the corresponding vertexes by 3.66 units along the edges and the actual length of the path is 30.1194 units - just a smidgen north of the first hunch 30-unit center to center length. But I guess for a snail even that counts ...
Nice visualization of the trails.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print
cuboid_paths.pdf