wu :: forums « wu :: forums - Triangular Numbers. » Welcome, Guest. Please Login or Register. Nov 24th, 2024, 7:27pm

RIDDLES SITE WRITE MATH! Home Help Search Members Login Register

wu :: forums    riddles    easy (Moderators: SMQ, Eigenray, towr, william wu, ThudnBlunder, Icarus, Grimbal)    Triangular Numbers. « Previous topic | Next topic » Pages: 1  Reply Notify of replies Send Topic Print    Author  Topic: Triangular Numbers.  (Read 2382 times) rloginunix Uberpuzzler     Posts: 1029 Triangular Numbers.   « on: Jan 9th, 2015, 7:54am » Quote Modify Triangular Numbers (a small generalization I came up with).   Express the length of a rubber band stretched over tangent unit circles forming an equilateral triangle as a function of the number of circles.   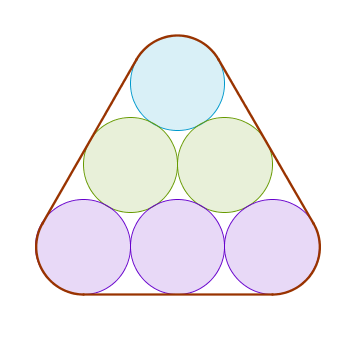A sample formation for T3 = 6 is shown below (Tn is a triangular number):       (one can generalize further for square, pentagonal, hexagonal numbers, etc.) IP Logged jollytall Senior Riddler     Gender: Posts: 585 Re: Triangular Numbers.   « Reply #1 on: Jan 11th, 2015, 9:54am » Quote Modify I would assume that for the n-th number it is 1+6*(n-1) IP Logged towr wu::riddles Moderator Uberpuzzler Some people are average, some are just mean.     Gender: Posts: 13730 Re: Triangular Numbers.   « Reply #2 on: Jan 11th, 2015, 1:04pm » Quote Modify I'd add a bit of pi to that. IP Logged Wikipedia, Google, Mathworld, Integer sequence DB rloginunix Uberpuzzler     Posts: 1029 Re: Triangular Numbers.   « Reply #3 on: Jan 11th, 2015, 4:30pm » Quote Modify I think it's just a typo. IP Logged jollytall Senior Riddler     Gender: Posts: 585 Re: Triangular Numbers.   « Reply #4 on: Jan 11th, 2015, 9:20pm » Quote Modify I wanted to be too quick . So it is 1 full circle + the 6*(n-2) straight diameters. It is therefore not only a bit of Pi, but 2 of them: 2Pi+6*(n-1).   And reading the question, it has to be expressed in the number of circles, so the above formula is correctly 2Pi+6*(Tn-2).   And Tn=n*(n+1)/2, n=(sqrt(8Tn+1)-1)/2 And thus the solution is   2Pi+3*sqrt(8Tn+1)-9 IP Logged rloginunix Uberpuzzler     Posts: 1029 Re: Triangular Numbers.   « Reply #5 on: Jan 11th, 2015, 10:39pm » Quote Modify That's right.   Another, less proper but may be intuitively more clear way to put it is to recall that the sum of any two consecutive triangular numbers is a perfect square:   2(Pi + 3(sqrt(Tn + Tn+1) - 2)) IP Logged Pages: 1  Reply Notify of replies Send Topic Print Forum Jump: ----------------------------- riddles -----------------------------=> easy   - medium   - hard   - what am i   - what happened   - microsoft   - cs   - putnam exam (pure math)   - suggestions, help, and FAQ   - general problem-solving / chatting / whatever ----------------------------- general -----------------------------  - guestbook   - truth   - complex analysis   - wanted   - psychology   - chinese « Previous topic | Next topic »

Powered by YaBB 1 Gold - SP 1.4!
Forum software copyright © 2000-2004 Yet another Bulletin Board