 Author
Author |
Topic: soccer tournament (Read 949 times) |
|
black_death
Newbie


Gender: 
Posts: 40
|
 |
soccer tournament
« on: May 6th, 2008, 12:06am » |
 Quote Quote  Modify Modify
|
In a soccer tournament n teams play against one another exactly once. The win fetches 3 points, draw 1 each and loss 0. After all the matches were played, it was noticed that the top team had unique number of maximum points and unique least number of wins (that is all other teams win more matches than the top team). What can be the minimum possible value of n ? (n>1)
|
| « Last Edit: May 8th, 2008, 7:49am by black_death » |
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: soccer tournament
« Reply #1 on: May 6th, 2008, 9:45am » |
 Quote Quote  Modify Modify
|
on May 6th, 2008, 12:06am, black_death wrote:| In a soccer tournament n teams play against one another exactly once. The win fetches 3 points, draw 1 each and loss 0. After all the matches were played, it was noticed that the top team had unique number of maximum points and unique least number of wins. What can be the minimum possible value of n? |
|
1
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: soccer tournament
« Reply #2 on: May 6th, 2008, 11:33am » |
 Quote Quote  Modify Modify
|
on May 6th, 2008, 9:45am, rmsgrey wrote:
How do they play 'exactly once'? 
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Random Lack of Squiggily Lines
Senior Riddler
   

Everything before 7/1/2008 is now irrelevant.
Gender: 
Posts: 460
|
 |
Re: soccer tournament
« Reply #3 on: May 6th, 2008, 1:05pm » |
 Quote Quote  Modify Modify
|
2
|
| « Last Edit: May 6th, 2008, 1:06pm by Random Lack of Squiggily Lines » |
 IP Logged IP Logged |
You can only believe i what you can prove, and since you have nothing proven to cmpare to, you can believe in nothing.
I have ~50 posts to hack a "R" into a "D". Which one?
|
|
|
black_death
Newbie


Gender: 
Posts: 40
|
 |
Re: soccer tournament
« Reply #4 on: May 6th, 2008, 6:57pm » |
 Quote Quote  Modify Modify
|
i think the question should be clarified further .... minimum number of wins mean that all the team win more matches than the top team
|
|
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: soccer tournament
« Reply #5 on: May 7th, 2008, 5:10am » |
 Quote Quote  Modify Modify
|
on May 6th, 2008, 11:33am, ThudanBlunder wrote:
How do they play 'exactly once'?  |
|
They play each and every other team exactly once each
|
|
 IP Logged IP Logged |
|
|
|
FiBsTeR
Senior Riddler
   


Gender: 
Posts: 581
|
 |
Re: soccer tournament
« Reply #6 on: May 7th, 2008, 2:40pm » |
 Quote Quote  Modify Modify
|
Why not zero teams?
I say that each team plays each other exactly once, for, if not, there would exist some team that played another team less than or greater than once, which contradicts the fact that there are no teams.
I say that the top team has the maximum number of points and the least number of wins, for, if not, there would exist either a team with more points or a team with less wins, which contradicts the fact that there are no teams.
Thus having zero teams fulfills all the requirements, and there clearly can't be a negative number of teams, so zero is the minimum. 
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: soccer tournament
« Reply #7 on: May 7th, 2008, 2:53pm » |
 Quote Quote  Modify Modify
|
on May 7th, 2008, 2:40pm, FiBsTeR wrote:
...and there clearly can't be a negative number of teams. |
|
Why not? I don't think, and I'm sure rmsgrey will back me up here, this has been ruled out in the problem statement. 
And who said the number of teams must be real?
For example, there might be i teams. In which case we would have      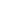 Tournament. Tournament.
|
| « Last Edit: May 8th, 2008, 5:51am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
black_death
Newbie


Gender: 
Posts: 40
|
 |
Re: soccer tournament
« Reply #8 on: May 7th, 2008, 6:47pm » |
 Quote Quote  Modify Modify
|
he he guys ..... ok the number of teams are greater than 1 
|
|
 IP Logged IP Logged |
|
|
|
Random Lack of Squiggily Lines
Senior Riddler
   

Everything before 7/1/2008 is now irrelevant.
Gender: 
Posts: 460
|
 |
Re: soccer tournament
« Reply #9 on: May 8th, 2008, 4:10am » |
 Quote Quote  Modify Modify
|
on May 6th, 2008, 1:05pm, Qaster Qof Qeverything Q42 wrote:
ahem
|
|
 IP Logged IP Logged |
You can only believe i what you can prove, and since you have nothing proven to cmpare to, you can believe in nothing.
I have ~50 posts to hack a "R" into a "D". Which one?
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: soccer tournament
« Reply #10 on: May 8th, 2008, 5:28am » |
 Quote Quote  Modify Modify
|
2 teams is impossible.
With 1 match, either it's a draw, in which case there's no unique winning team, or one team wins, in which case the unique winning team has more wins than some other team...
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: soccer tournament
« Reply #11 on: May 9th, 2008, 9:47am » |
 Quote Quote  Modify Modify
|
But getting real,
let top team win w times.
Then top team has (n-1) - w draws.
Now if top team has k wins less than another team then
top team must have at least 3k+1 more draws than the other team in order to end up with more points.
More draws requires more matches, which require more teams in the tournament.
So assume minimum is achieved when top team has just one less win than every other team.
Then top team must draw at least 4 more games than every other team, in order to end up with more points.
And some other teams have drawn at least one game (eg. with top team).
So
n - 1 - w > 4
n > w + 5 .........................................(1)
And if all except top team score w+1 wins
then total number of wins
= total number of losses
= n(w+1) - 1
And top team has n - 1 - w draws.
So considering total number of games we get
2n(w+1) - 2 + 2(n-1-w)  n(n-1) n(n-1)
or
n2 - (2w+5)n + 2w + 4 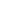 0 0
(n - 1)(n - 2w - 4) 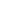 0 0
And n = 1 gives us rsmgrey's deep observation. 
Otherwise n 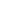 2w + 4 2w + 4
Putting w = 1 gives n 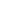 6 6
But n > 6 by (1)
Finally, putting w = 2 gives n 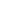 8 8
Team 1: W - W - D - D - D - D - D (11 points)
Team 2: W - W - W - D - L - L - L (10 points)
Team 3: W - W - W - D - L - L - L (10 points)
Team 4: W - W - W - D - L - L - L (10 points)
Team 5: W - W - W - D - L - L - L (10 points)
Team 6: W - W - W - D - L - L - L (10 points)
Team 7: W - W - W - L - L - L - L ( 9 points)
Team 8: W - W - W - L - L - L - L ( 9 points)
It's nice to get one all to myself. And I'm glad I managed to finish it before Hippo arrived. 
|
| « Last Edit: May 10th, 2008, 10:58am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
black_death
Newbie


Gender: 
Posts: 40
|
 |
Re: soccer tournament
« Reply #12 on: May 9th, 2008, 11:57am » |
 Quote Quote  Modify Modify
|
Perfect TB 
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: soccer tournament
« Reply #13 on: May 9th, 2008, 12:10pm » |
 Quote Quote  Modify Modify
|
on May 9th, 2008, 9:47am, ThudanBlunder wrote:
Team 1: W - W - D - D - D - D - D (11 points)
Team 2: W - W - W - D - L - L - L (10 points)
Team 3: W - W - W - D - L - L - L (10 points)
Team 4: W - W - W - D - L - L - L (10 points)
Team 5: W - W - W - D - L - L - L (10 points)
Team 6: W - W - W - D - L - L - L (10 points)
Team 7: W - W - W - L - L - L - L (10 points)
Team 8: W - W - W - L - L - L - L (10 points)
|
|
Except the number of points of last two teams
on May 9th, 2008, 9:47am, ThudanBlunder wrote:
It's nice to get one all to myself. And I'm glad I managed to finish it before Hippo arrived. 
|
|
 I have resign to write answers (and even to solve) such an amount of riddles ... at least few first days I have resign to write answers (and even to solve) such an amount of riddles ... at least few first days
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: soccer tournament
« Reply #14 on: May 9th, 2008, 12:37pm » |
 Quote Quote  Modify Modify
|
on May 9th, 2008, 12:10pm, Hippo wrote:
Except the number of points of last two teams
|
|
Thanks. Now corrected.
on May 9th, 2008, 11:57am, black_death wrote:Perfect TB  |
|
There is a small step missing.
I haven't yet proved that n=7, w=1 is not possible (and it doesn't seem to be - it leaves too many draws).
|
| « Last Edit: May 10th, 2008, 5:56pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: soccer tournament
« Reply #15 on: May 10th, 2008, 6:38pm » |
 Quote Quote  Modify Modify
|
on May 9th, 2008, 12:37pm, ThudanBlunder wrote:
There is a small step missing.
I haven't yet proved that n=7, w=1 is not possible (and it doesn't seem to be - it leaves too many draws).
|
|
OK, I think I have it.
The top team draws n - 1 - w games
and they draw at least 4 more games than every other team.
So no other team can draw more than n - 5 - w games.
So the total number of draws (times 2) must be less than or equal to
(n - 1)(n - 5 - w) + (n - 1 - w)
= n(n - 5 - w) + 4
And total number of draws (times 2) = total number of games (times 2) - total number of wins - total number of losses
So we have
n(n - 1) - 2n(w + 1) + 2 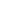 n(n - 5 - w) + 4 n(n - 5 - w) + 4
And this simplifies to
(2 - w)n 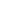 2 2
And we know that n > w + 5 or n = 1
When n = 1, w = 0, trivially.
And n > w + 5 leads to
(2 - w)(w + 5) < 2
and so w 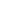 2 2
QED
|
| « Last Edit: Jun 3rd, 2008, 6:38am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register