 Author
Author |
Topic: Another Flawed Proof (Read 989 times) |
|
FiBsTeR
Senior Riddler
   


Gender: 
Posts: 581
|
 |
Another Flawed Proof
« on: Nov 30th, 2007, 10:03am » |
 Quote Quote  Modify Modify
|
I walked into school this afternoon and I saw the following flawed proof on the board:
::::
 (-1) (-1) 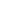  (-1) = (-1) =  (-1 (-1 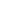 -1) -1)
i 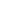 i = i =  (1) (1)
-1 = 1
::::
This problem is (I think) similar to the one here. yet I still can't convince myself what the flaw is...
I believe the first line is wrong, but does this mean that multiplying the radicands doesn't work for negative numbers? The thread I linked to above might suggest that we are not "choosing" the correct parity of the root, but that concept of choosing which root still doesn't sit well with me. 
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: Another Flawed Proof
« Reply #1 on: Nov 30th, 2007, 1:27pm » |
 Quote Quote  Modify Modify
|
Obviously, if r2=x then (-r)2=x also. That means that for every square root r, -r is just as good a square root.
As long as you deal with reals, you can define sqrt(x) to be the positive root. And the square root of a negative number "does not exist". In that case, you have the convenient property that sqrt(x·y) = sqrt(x)·sqrt(y). But in the complex plane, it is less obvious which one of the roots is "better" than the other. You have to choose one. And depending which root you choose for sqrt(x), sqrt(y) and sqrt(x·y), you might well find out that sqrt(x·y) = -sqrt(x)·sqrt(y)
|
| « Last Edit: Dec 1st, 2007, 2:45am by Grimbal » |
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Another Flawed Proof
« Reply #2 on: Nov 30th, 2007, 7:58pm » |
 Quote Quote  Modify Modify
|
Someone easily slipped you up with this.
The first statement is the flaw. That is, it is not true,
and so neither are the two thereafter. No matter
your choice of sign in any subsequent expressions
after the first statement, you are working with a
false statement to begin with.
I believe that Grimbal's example tells you that if
you can select a sign for a square root then you
may as well accept the first statement as being
true.
Riddle: for x and y real or complex, is it true that
the real part of sqrt(x*y) is >= 0?
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
JiNbOtAk
Uberpuzzler
    

Hana Hana No Mi
Gender: 
Posts: 1187
|
 |
Re: Another Flawed Proof
« Reply #3 on: Nov 30th, 2007, 9:48pm » |
 Quote Quote  Modify Modify
|
on Nov 30th, 2007, 7:58pm, Michael_Dagg wrote:Riddle: for x and y real or complex, is it true that
the real part of sqrt(x*y) is >= 0? |
|
Umm, yeah, otherwise it would be imaginary, right ?
|
|
 IP Logged IP Logged |
Quis custodiet ipsos custodes?
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Another Flawed Proof
« Reply #4 on: Dec 1st, 2007, 12:49am » |
 Quote Quote  Modify Modify
|
> Umm, yeah, otherwise it would be imaginary, right ?
Pretty good question.
Let x,y be given. If you were to write sqrt(x*y) how would you do it?
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
FiBsTeR
Senior Riddler
   


Gender: 
Posts: 581
|
 |
Re: Another Flawed Proof
« Reply #5 on: Dec 1st, 2007, 11:55am » |
 Quote Quote  Modify Modify
|
I guess you're really hitting on where I'm misunderstanding this:
My interpretation of writing "sqrt()" is that you're taking the root that has a positive real part. So no matter what the radicand is, writing "sqrt()" implies that the real part is positive. For real radicands you would say this is the principle root/value, though I'm not sure if this can be used for complex radicands. Otherwise, you would write "-sqrt()" to imply the other root. Is this a misinterpretation?
EDIT: To throw in numbers to your example, let x = y = -3 + 2i. I say that sqrt(xy) = 3 - 2i, and Re(sqrt(xy)) = 3 > 0. If I wanted -sqrt(xy), I'd have Re(-sqrt(xy)) = -3 < 0.
|
| « Last Edit: Dec 1st, 2007, 12:03pm by FiBsTeR » |
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: Another Flawed Proof
« Reply #6 on: Dec 1st, 2007, 11:59pm » |
 Quote Quote  Modify Modify
|
In that case, sqrt(a·b) = sqrt(a)·sqrt(b) is simply not true.
If a = b = -3+4i
sqrt(a) = sqrt(b) = 1+2i (with Re()>0)
sqrt(a)·sqrt(b) = -3+4i
but sqrt(ab) = 3-4i (chosen with Re()>0)
But you are using sqrt(a·b) = sqrt(a)·sqrt(b) in the first line of the proof.
As Michael said: The first statement is the flaw.
|
| « Last Edit: Dec 2nd, 2007, 12:05am by Grimbal » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register