 Author
Author |
Topic: Divide two expressions, get perfect square? (Read 1729 times) |
|
K Sengupta
Senior Riddler
   

Gender: 
Posts: 371
|
 |
Divide two expressions, get perfect square?
« on: Jul 27th, 2007, 8:06am » |
 Quote Quote  Modify Modify
|
Analytically determine whether there exists any pair of positive integers (x, y) satisfying:
(x2000 – 1)/(x-1) = y2
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Divide two expressions, get perfect square?
« Reply #1 on: Jul 31st, 2007, 10:58am » |
 Quote Quote  Modify Modify
|
I must be missing the "easy" solution! First observe:
| hidden: | x2000-1 =   n(x), n(x),
where the product is over divisors n of 2000, and  n is the n-th cyclotomic polynomial. n is the n-th cyclotomic polynomial.
Now, for n 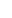 m, m,  n and n and  m are relatively prime, since they are both irreducible, and therefore 1 is a linear combination of m are relatively prime, since they are both irreducible, and therefore 1 is a linear combination of  n and n and  m, with coefficients in m, with coefficients in 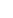 [x]. Clearing denominators, we get a relation of the form d = f [x]. Clearing denominators, we get a relation of the form d = f  n + g n + g  m, where d is an integer, and f,g m, where d is an integer, and f,g  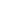 [x]. Then for any integer x, gcd( [x]. Then for any integer x, gcd( n(x), n(x),  m(x)) must divide d. For any given n,m, this value d can be found using the Euclidean algorithm, and it turns out that for n,m divisors of 2000, d is either 1,2, or 5. m(x)) must divide d. For any given n,m, this value d can be found using the Euclidean algorithm, and it turns out that for n,m divisors of 2000, d is either 1,2, or 5. |
Here's a question (but this goes beyond easy, I'm sure): find a closed form for d, in terms of n and m.
Anyway, given the above, lets find all integer solutions:| hidden: |
Since any two factors  n(x) and n(x) and  m(x) have a gcd of 1,2, or 5, and the product is a square, it follows that each factor is of the form 2a5b*y2, where a,b are either 0 or 1. [Note that for n>2, m(x) have a gcd of 1,2, or 5, and the product is a square, it follows that each factor is of the form 2a5b*y2, where a,b are either 0 or 1. [Note that for n>2,  n(x)>0 for all x, since it has no real root.] n(x)>0 for all x, since it has no real root.]
Since  8(x) = x4+1 is never divisible by 5, it is either a square, or twice a square. But if x4+1=y2, then 1=y2-x4 is the difference of two squares, which happens only for y2=1, x=0. Aside from this solution, we can conclude therefore that x4+1 is twice a square, and therefore x is odd. 8(x) = x4+1 is never divisible by 5, it is either a square, or twice a square. But if x4+1=y2, then 1=y2-x4 is the difference of two squares, which happens only for y2=1, x=0. Aside from this solution, we can conclude therefore that x4+1 is twice a square, and therefore x is odd.
Now observe that  5(x) = 1+x+x2+x3+x4, and 5(x) = 1+x+x2+x3+x4, and  10(x) = 10(x) =  5(-x) are always odd. Moreover, 5(-x) are always odd. Moreover,  5(x) is divisible by 5 iff x=1 mod 5, and 5 | 5(x) is divisible by 5 iff x=1 mod 5, and 5 |  10(x) iff x=-1 mod 5. WLOG, then (replacing x with -x if necessary), 10(x) iff x=-1 mod 5. WLOG, then (replacing x with -x if necessary),  5(x) is not divisible by 5. 5(x) is not divisible by 5.
It follows now that  5(x) must be a square. But! x is odd, and 5(x) must be a square. But! x is odd, and
(x2+(x-1)/2)2 < x4+x3+x2+x+1 < (x2+(x+1)/2)2,
since the difference on the left is 7x2/4+3x/2+3/4 > 0, and the difference on the right is x2/4 - x/2 - 3/4 > 0 when x < -1, or x > 3. This leaves only x=-1,1,3 to consider, which is straightforward. |
Thus the only integer solutions are (0, 1), and (-1, 0). Phew! 1), and (-1, 0). Phew!
|
| « Last Edit: Aug 5th, 2007, 12:20am by Eigenray » |
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Divide two expressions, get perfect square?
« Reply #2 on: Jul 31st, 2007, 12:16pm » |
 Quote Quote  Modify Modify
|
Can't we do something with (x2000 – 1)/(x-1) =  1999i=0 xi? 1999i=0 xi?
[e] If I'm not mistaken xi mod m is periodic with period m or some smaller factor of it. So among other things (x2000 – 1)/(x-1) should be 0 modulo every m that divides 2000. Right? But is that remotely useful... hmm[/e]
|
| « Last Edit: Jul 31st, 2007, 12:39pm by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Divide two expressions, get perfect square?
« Reply #3 on: Jul 31st, 2007, 3:40pm » |
 Quote Quote  Modify Modify
|
I'm not sure what.
If 2000 were odd, say f(x) is a monic polynomial of even degree 2n, we could expand  f(x) = g(x) + O(1/x), where g is a polynomial with rational coefficients of degree n. If f is not a perfect square, then f(x) - g(x)2 = c*xk + O(xk-1), with c f(x) = g(x) + O(1/x), where g is a polynomial with rational coefficients of degree n. If f is not a perfect square, then f(x) - g(x)2 = c*xk + O(xk-1), with c 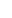 0, and k < n. 0, and k < n.
For each congruence class of x mod the LCM of the denominators of g's coefficients, find a rational t, 0  t t  1, such that g(x)-t is integer (don't take t=1 if c>0, nor t=0 if c<0). Then 1, such that g(x)-t is integer (don't take t=1 if c>0, nor t=0 if c<0). Then
(g(x)-t)2 < f(x) < (g(x)+1-t)2
for x sufficiently large. More generally, I guess if f(x) is monic of degree kn, and is not a perfect k-th power, then f(x)=yk has only finitely many solutions, which can be found constructively? (Sounds right but if so I'm surprised I didn't know that.)
I didn't get anywhere considering (x2000-1)/(x-1) mod m for various m.
|
|
 IP Logged IP Logged |
|
|
|
K Sengupta
Senior Riddler
   

Gender: 
Posts: 371
|
 |
Re: Divide two expressions, get perfect square?
« Reply #4 on: Aug 6th, 2007, 8:05am » |
 Quote Quote  Modify Modify
|
A proposed solution is furnished hereunder as follows:
Substituting (a, b, c) = {x^1000 + 1, x^500 + 1, (x^500 – 1)/(x-1)}
we obtain:
(x^2000 – 1)/(x-1) = abc
Now b and c divide a-2, while c divides b-2.
Accordingly, it follows that the gcd of any two of a, b and c is at most 2.
The product abc is a perfect square if a, b and c are either squares or doubles of squares.
It is clearly observed that neither a nor b can be squares of positive integers.
Accordingly, each of a and b must correspond to twice the square of positive integers.
Therefore, we must have:
4ab = 4*x^1500 + 4*x^1000 + 4*x^500 + 4 must be a perfect square.
However, in that situation:
(2*x^750 + x^250)^2 < 4*x^1500 + 4*x^1000 + 4*x^500 + 4
< (2*x^750 + x^250 + 1)^2
This implies that 4ab is not a perfect square, which leads to a contradiction.
Consequently, the given equation does not admit of positive integer solutions.
Of course, the non negative integer solutions are indeed : (0, +/-1), and (-1, 0) as rightly pointed out by Eigenray.
In conclusion, I personally consider the above solution in terms of the current post to be much inferior in quality when compared to Eigenray's superior methodology.
|
| « Last Edit: Aug 6th, 2007, 9:37am by K Sengupta » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Divide two expressions, get perfect square?
« Reply #5 on: Aug 7th, 2007, 6:21am » |
 Quote Quote  Modify Modify
|
on Aug 6th, 2007, 8:05am, K Sengupta wrote:| In conclusion, I personally consider the above solution in terms of the current post to be much inferior in quality when compared to Eigenray's superior methodology. |
|
 I don't know why you would say that. Yours is more elementary and only requires that 2000 = 8n. Mine only works for 2000 = 40n, where n is a product of powers of 2 and 5. I don't know why you would say that. Yours is more elementary and only requires that 2000 = 8n. Mine only works for 2000 = 40n, where n is a product of powers of 2 and 5.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register