 Author
Author |
Topic: Anyone For Tennis? (Read 9505 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Anyone For Tennis?
« on: May 9th, 2007, 6:19pm » |
 Quote Quote  Modify Modify
|
Two tennis players play a game where the server has probability p > 1/2 of winning any point and probability q of losing it, where p + q = 1
What is the probability that the server will win the game?
|
| « Last Edit: May 9th, 2007, 6:32pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
JiNbOtAk
Uberpuzzler
    

Hana Hana No Mi
Gender: 
Posts: 1187
|
 |
Re: Anyone For Tennis?
« Reply #1 on: May 9th, 2007, 6:30pm » |
 Quote Quote  Modify Modify
|
on May 9th, 2007, 6:19pm, ThudanBlunder wrote:
What is the probability that the server will the game?
|
|
Win or loose ?
|
|
 IP Logged IP Logged |
Quis custodiet ipsos custodes?
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Anyone For Tennis?
« Reply #2 on: May 9th, 2007, 6:33pm » |
 Quote Quote  Modify Modify
|
on May 9th, 2007, 6:30pm, JiNbOtAk wrote:
Thanks for pointing out my my omission (now corrected).
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Anyone For Tennis?
« Reply #3 on: May 13th, 2007, 9:55am » |
 Quote Quote  Modify Modify
|
Evidently not. 
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Anyone For Tennis?
« Reply #4 on: May 13th, 2007, 1:39pm » |
 Quote Quote  Modify Modify
|
I had gotten confused on the rules of scoring because they weren't what I remembered, but now I realize I was thinking of volleyball.
Let X,Y be the scores of players A,B, respectively, so with probability p, we increase X, and with probability q, we increase Y. Let S = X-Y.
First consider the simplified version where we stop as soon as |S|=2. Let ai be the probability that player A wins given S=i. We have
ai = p ai+1 + q ai-1,
giving a recurrence with characteristic polynomial pt2 - t + q = (t-1)(pt-q). So
ai = c + d ri,
where r=q/p. The initial condition a-2=0 gives c = -d/r2, and a2=1 gives d=1/(r2-1/r2), and so
a0 = (1-r2)/(1-r4) = p2/(p2+q2)
is the probability that A wins this simplified game. (This can also be deduced by considering the Martingale rS.)
It's possible for A to win the simplified game but still lose the real game, but there are only four five ways this can happen. Let (x,y) denote the score X=x, Y=y.
-We can "win" at (2,0) and lose at (2,2) in one way: (0,0)->(2,0)->(2,2). The probability that this happens is p2q2(1-a0), since the simplified game is the same as the real one starting at (2,2).
-We can "win" at (3,1), and lose at (3,3) in 4 ways: (3,0)->(3,3), or (2,0)->(2,1)->(3,1)->(3,3), or (1,0)->(1,1)->(3,1)->(3,3) or (0,1)->(3,1)->(3,3). The probability that this happens is 4p3q3(1-a0).
So the probability that A wins the simplified game but loses the real game is
(1-a0)(p2q2+4p3q3).
And similarly, the probability that A loses the simplified game but wins the real game is
a0(p2q2 + 4p3q3).
So the overall probability is
a0 + (2a0-1)(p2q2+4p3q3)
= p2/(p2+q2) [ 1 + (p2-q2)(pq)2(1+4pq) ]
... I think.
|
| « Last Edit: May 13th, 2007, 8:12pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Anyone For Tennis?
« Reply #5 on: May 13th, 2007, 4:23pm » |
 Quote Quote  Modify Modify
|
Thanks for your reply, Eigenray.
1) In tennis a game is won by the first player to win 4 points, unless the score gets to 3-3 (this is called deuce), in which case the game continues until one of the players gets two points ahead.
2) The solution method and answer, a function of p and/or q, are quite simple.
|
| « Last Edit: May 13th, 2007, 5:42pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Anyone For Tennis?
« Reply #6 on: May 13th, 2007, 7:59pm » |
 Quote Quote  Modify Modify
|
Upon further consideration (solving a linear system in 15 variables), I get
p4(1+2q(2-p)+2q2(5-4p))/(1-2pq),
which agrees with experiment. But I still don't see the error in my previous approach. and my previous solution.
What if they play until one person has at least A points and is ahead by at least B points (tennis: A=4,B=2)?
|
| « Last Edit: May 13th, 2007, 8:15pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Anyone For Tennis?
« Reply #7 on: May 13th, 2007, 8:45pm » |
 Quote Quote  Modify Modify
|
on May 13th, 2007, 7:59pm, Eigenray wrote:Upon further consideration (solving a linear system in 15 variables), I get
p4(1+2q(2-p)+2q2(5-4p))/(1-2pq),? |
|
For normal tennis, employing 1 independent variable, I get p4 + 4p4q + [(10p4q2/(1 - 2pq)]
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Anyone For Tennis?
« Reply #8 on: May 13th, 2007, 10:06pm » |
 Quote Quote  Modify Modify
|
It's the same, but written like that it's much more obvious:
p4 is the probability of winning at (4,0).
4p4q is the probability of winning at (4,1), since you can get to (3,1) in C(3+1,1) ways.
10p4q2 is the probability of winning at (4,2), since you can get to (3,2) in C(3+2,2) ways.
20p5q3 is the probability of winning at (5,3), since you can get to (4,3) in C(4+3,3) ways.
And for n 4, #[ways to win at (n+2,n)] = #[ways to get to (n,n)] = 2#[ways to get to (n-1,n-1)] = 2#[ways to win at (n+1,n-1)]. So the probability of winning is 4, #[ways to win at (n+2,n)] = #[ways to get to (n,n)] = 2#[ways to get to (n-1,n-1)] = 2#[ways to win at (n+1,n-1)]. So the probability of winning is
p4 + 4p4q + 10p4q2 + 20p5q3 + 40p6q4 + ...
= p4 + 4p4q + 10p4q2/(1-2pq).
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Anyone For Tennis?
« Reply #9 on: May 13th, 2007, 10:29pm » |
 Quote Quote  Modify Modify
|
Your generalisation is also interesting and will cover tie-breaks when the server is assumed to have no advantage (which is probably quite true for many occasional players).
|
| « Last Edit: May 16th, 2007, 11:43am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Anyone For Tennis?
« Reply #10 on: May 20th, 2007, 8:16pm » |
 Quote Quote  Modify Modify
|
on May 13th, 2007, 8:45pm, ThudanBlunder wrote:
For normal tennis, employing 1 independent variable, I get p4 + 4p4q + [(10p4q2/(1 - 2pq)] |
|
For example, when p = 2/3, q = 1/3, the server wins with probability 208/243, roughly a 6 in 7 chance.
on May 13th, 2007, 7:59pm, Eigenray wrote:| What if they play until one person has at least A points and is ahead by at least B points (tennis: A=4,B=2)? |
|
Probability of winning without reaching deuce
equals
Probability of winning by A points to r (for r = 0 to A-B)
equals
pA + A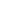 1pAq + A+1 1pAq + A+1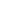 2pAq2 + A+2 2pAq2 + A+2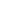 3pAq3+ ...... + 2A-B-1 3pAq3+ ...... + 2A-B-1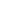 A-BpAqA-B A-BpAqA-B
When deuces are considered, as the value of B does not affect the common ratio, which remains 2pq,
the required probability equals
pA + A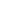 1pAq + A+1 1pAq + A+1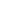 2pAq2 + A+2 2pAq2 + A+2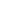 3pAq3 + ...... + [2A-B-1 3pAq3 + ...... + [2A-B-1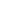 A-BpAqA-B/(1-2pq)] A-BpAqA-B/(1-2pq)]
For example, in a tie-break (A = 7, B = 2) this gives probability of winning to be
p7 + 7p7q + 28p7q2 + 84p7q3 + 210p7q4 + [462p7q5/(1 - 2pq)]
|
| « Last Edit: Feb 1st, 2009, 4:57am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Anyone For Tennis?
« Reply #11 on: Sep 5th, 2007, 11:07pm » |
 Quote Quote  Modify Modify
|
Clearly it's more than 1/2. And thunderblunder, why answer your own question then quote yourself on it.
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Anyone For Tennis?
« Reply #12 on: Sep 6th, 2007, 1:58am » |
 Quote Quote  Modify Modify
|
on Sep 5th, 2007, 11:07pm, srn347 wrote:| Clearly it's more than 1/2. And thunderblunder, why answer your own question then quote yourself on it. |
|
I answered my own question because my answer appeared to differ from Eigenray's.
I quoted my answer in order to give a specific example with p = 2/3, q = 1/3
You would have realized this if you had listened to Mummy and taken your Ritalin before posting.
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Anyone For Tennis?
« Reply #15 on: Sep 6th, 2007, 8:02pm » |
 Quote Quote  Modify Modify
|
Do I dare search?
|
|
 IP Logged IP Logged |
|
|
|
ima1trkpny
Senior Riddler
   

"Double click on 'Yes'... Hey!"
Gender: 
Posts: 452
|
 |
Re: Anyone For Tennis?
« Reply #16 on: Sep 6th, 2007, 10:59pm » |
 Quote Quote  Modify Modify
|
on Sep 6th, 2007, 8:02pm, srn347 wrote:
Do I really have to do your work for you so you can understand what was implied?? 
Ritalin is the brand name of methylphenidate, a drug commonly used to tread ADHD. I'm rather suprised you've never heard of it... as it is pretty common... but even if you've never come across it, it is easy enough to find out about. No excuse for being lazy...
|
|
 IP Logged IP Logged |
"The pessimist sees difficulty in every opportunity. The optimist sees the opportunity in every difficulty." -Churchill
|
|
|
mikedagr8
Uberpuzzler
    

A rich man is one who is content; not wealthy.
Gender: 
Posts: 1105
|
 |
Re: Anyone For Tennis?
« Reply #17 on: Sep 7th, 2007, 3:11am » |
 Quote Quote  Modify Modify
|
on Sep 6th, 2007, 10:59pm, ima1trkpny wrote:
Do I really have to do your work for you so you can understand what was implied?? 
Ritalin is the brand name of methylphenidate, a drug commonly used to tread ADHD... No excuse for being lazy... |
|
Someone with ADHD really has no excuse.
|
|
 IP Logged IP Logged |
"It's not that I'm correct, it's that you're just not correct, and so; I am right." - M.P.E.
|
|
|
mikedagr8
Uberpuzzler
    

A rich man is one who is content; not wealthy.
Gender: 
Posts: 1105
|
 |
Re: Anyone For Tennis?
« Reply #18 on: Sep 7th, 2007, 4:35am » |
 Quote Quote  Modify Modify
|
on Sep 6th, 2007, 5:13pm, ThudanBlunder wrote:
Ever heard of Google, sonny?
|
|
Don't think he has ever listened, so it doesn't surprise me that he hasn't, as everyone else is, I am sure.
|
| « Last Edit: Sep 7th, 2007, 4:35am by mikedagr8 » |
 IP Logged IP Logged |
"It's not that I'm correct, it's that you're just not correct, and so; I am right." - M.P.E.
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Anyone For Tennis?
« Reply #19 on: Sep 7th, 2007, 6:06pm » |
 Quote Quote  Modify Modify
|
Get back on topic. Is that p^4+q^2+10p^4q^2/1-2pq thing provable?
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Anyone For Tennis?
« Reply #20 on: Sep 7th, 2007, 6:13pm » |
 Quote Quote  Modify Modify
|
on Sep 7th, 2007, 6:06pm, srn347 wrote:| Get back on topic. Is that p^4+q^2+10p^4q^2/1-2pq thing provable? |
|
Would you even recognise a proof if you found one in your cornflakes??
|
| « Last Edit: Sep 7th, 2007, 6:17pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
ima1trkpny
Senior Riddler
   

"Double click on 'Yes'... Hey!"
Gender: 
Posts: 452
|
 |
Re: Anyone For Tennis?
« Reply #21 on: Sep 7th, 2007, 6:27pm » |
 Quote Quote  Modify Modify
|
on Sep 7th, 2007, 6:13pm, ThudanBlunder wrote:
Would you even recognise a proof if you found one in your cornflakes??
|
|
T&B, how 'bout we consider giving him another shot... and be a tad kinder... I have a feeling he doesn't really know any better. I think we all understand the vexation, but let's give him one more shot now that it has been made clear what our issues with him are. Fair enough?
|
|
 IP Logged IP Logged |
"The pessimist sees difficulty in every opportunity. The optimist sees the opportunity in every difficulty." -Churchill
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Anyone For Tennis?
« Reply #22 on: Sep 7th, 2007, 6:30pm » |
 Quote Quote  Modify Modify
|
on Sep 7th, 2007, 6:27pm, ima1trkpny wrote:
T&B, how 'bout we consider giving him another shot... and be a tad kinder... I have a feeling he doesn't really know any better. |
|
Yeah, you are right. I shouldn't mock the afflicted.
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
mikedagr8
Uberpuzzler
    

A rich man is one who is content; not wealthy.
Gender: 
Posts: 1105
|
 |
Re: Anyone For Tennis?
« Reply #23 on: Sep 8th, 2007, 1:51am » |
 Quote Quote  Modify Modify
|
on Sep 7th, 2007, 6:30pm, ThudanBlunder wrote:
Yeah, you are right. I shouldn't mock the afflicted.
|
|
It's hard to control yourself sometimes, for anyone who has more to give TB for his attitude.
|
|
 IP Logged IP Logged |
"It's not that I'm correct, it's that you're just not correct, and so; I am right." - M.P.E.
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Anyone For Tennis?
« Reply #24 on: Sep 8th, 2007, 8:20am » |
 Quote Quote  Modify Modify
|
And have you taken your ritalin, thunderblunder(pun intended)? Now were even.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register