Author |
Topic: Triangles, Pentagons, and Hexagons (Read 2692 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Triangles, Pentagons, and Hexagons
« on: May 8th, 2007, 8:36am » |
 Quote  Modify
|
1) If you choose a number at random from Pascal's triangle (and not just a finite segment of it) what is the probability that it will be odd?
2) In order to make a regular polyhedron from pentagons and hexagons how many pentagons will you need?
|
| « Last Edit: May 8th, 2007, 8:25pm by ThudnBlunder » |
 IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #1 on: May 8th, 2007, 8:43am » |
Quote Modify
|
1) The same probability that a random integer is odd, depending on your method of random selection. 
2) always 12, if I recall correctly
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #2 on: May 8th, 2007, 8:46am » |
Quote Modify
|
1) Something like (3/4)infinity
2) There is a solution in 12, well known by even the less math-inclined people.
|
| « Last Edit: May 8th, 2007, 8:50am by Grimbal » |
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #3 on: May 8th, 2007, 9:21am » |
Quote Modify
|
on May 8th, 2007, 8:43am, towr wrote:| 1) The same probability that a random integer is odd, depending on your method of random selection. |
|
That sounds like 1/2 to me. 
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #4 on: May 8th, 2007, 9:53am » |
Quote Modify
|
on May 8th, 2007, 9:21am, ThudanBlunder wrote:| That sounds like 1/2 to me. |
|
It should sound like "whatever you want"
Consider the set of (non-negative) integers {4i+1, 4i+3, 2i | i  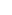 }. If you pick uniformly random from the set with i's up to n, then odd numbers are twice as likely as even numbers.
Picking (uniformly) randomly from an infinite set often has these problems.
If you pick the typical way of constructing Pascals's triangle as basis for growing the multiset, the limit of picking uniformly random from it should give the same probability as Grimbal.
|
| « Last Edit: May 8th, 2007, 9:59am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #5 on: May 8th, 2007, 9:57am » |
Quote Modify
|
I think my solution is the most natural one, even though there really isn't a natural way to choose a number randomly in Pascal's triangle. So Towr's answer is more correct.
|
| « Last Edit: May 8th, 2007, 9:58am by Grimbal » |
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #6 on: May 8th, 2007, 10:07am » |
Quote Modify
|
on May 8th, 2007, 9:57am, Grimbal wrote:| I think my solution is the most natural one, even though there really isn't a natural way to choose a number randomly in Pascal's triangle. So Towr's answer is more correct. |
|
Yes, I should have phrased the question differently.
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #7 on: May 8th, 2007, 10:12am » |
Quote Modify
|
on May 8th, 2007, 8:46am, Grimbal wrote:| 12) There is a solution in 12, well known by even the less math-inclined people. |
|
And, assuming the number of pentagons is indeed constant, the number needed with zero hexagons should be a dead giveaway to the math-inclined. 
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
on May 8th, 2007, 8:46am, Grimbal wrote:| 1) Something like (3/4)infinity |
|
Let p(n) be the probability that a number, picked uniformly from the first n rows of Pascal's triangle, is odd. If one looks at p(2x)*2(4/3)x, the graph quickly converges to the following (with period 1).
[How come Firefox and IE treat bgcolor="#252525" as #272A2F?]
|
| « Last Edit: Dec 22nd, 2008, 4:43am by Eigenray » |
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #9 on: May 8th, 2007, 1:32pm » |
Quote Modify
|
on May 8th, 2007, 8:46am, Grimbal wrote:| 2) There is a solution in 12, well known by even the less math-inclined people. |
|
Now that I think of it, few of them would actually know how many pentagons there are. Or even that there are any pentagons. 
|
|
IP Logged |
|
|
|
JohanC
Senior Riddler
Posts: 460
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #10 on: May 8th, 2007, 1:58pm » |
Quote Modify
|
on May 8th, 2007, 8:36am, ThudanBlunder wrote:| 2) In order to make a regular polyhedron from pentagons and hexagons how many pentagons will you need? |
|
For some kind of proof, I think we need to start with a well-known formula from
Descartes (but named after Euler).
That formula states:
V+F-E=2
Or "vertices + faces - edges = 2" for closed genus 0 polyhedra.
Next to that we probably also need to state that for every regular polyhedron consisting of pentagons and hexagons exactly 3 edges meet in every vertex. More than 3 would make the angle sum more than 360º. And less than 3 would be degenerate.
Putting things together:
- suppose we have h hexagons and p pentagons
- then we get E=(6*h+5*p)/2 and F=h+p
- the 3 edges meeting in every vertex can be written as V=E*2/3
- rewriting things we get
F - E/3 = 2
or h+p - (6*h+5*p)/2/3 = 2
or 6h+6p - (6*h+5*p) = 12
thus p=12
By the way, is there a special reason you put these two questions together?
Other than that Blaise Pascal and René Descartes are both famous philosophers living in 17th century France?
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #11 on: May 10th, 2007, 5:17am » |
Quote Modify
|
on May 8th, 2007, 1:58pm, JohanC wrote:
For some kind of proof, I think we need to start with a well-known formula from
Descartes (but named after Euler).
|
|
But didn't Descartes consider only vertices, faces, and plane angles? By omitting edges he couldn't have derived Euler's formula.
Well, I posted the puzzles together only because I thought they were too easy to deserve their own threads.
|
| « Last Edit: May 10th, 2007, 9:17am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
JohanC
Senior Riddler
Posts: 460
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #12 on: May 10th, 2007, 6:55am » |
Quote Modify
|
on May 10th, 2007, 5:17am, ThudanBlunder wrote:| But didn't Descartes consider only vertices, faces, and plane angles? By omitting edges he couldn't have derived Euler's formula. |
|
I got this information among other sources from Mathworld which has a high reputation but, of course, is not always correct.
However, I also encountered some historically reputed source with quite some detail at The Mathematical Association of America.
Quote:| I posted the puzzles together only because I thought they were too easy to deserve their own threads. |
|
Oh, I see. Wouldn't things be more organized having only one subject per thread?
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #13 on: May 11th, 2007, 4:23pm » |
Quote Modify
|
on May 10th, 2007, 6:55am, JohanC wrote:
Oh, I see. Wouldn't things be more organized having only one subject per thread?
|
|
True, but I knew that expert metagrobologists like Eigenray, towr, Grimbal, and SMQ would make short work of them (not to mention your own text-book solution to the second).
It seems to me from pages 4 and 5 of your excellent MAA link that Descartes didn't quite get there.
|
| « Last Edit: May 12th, 2007, 6:30am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
on May 11th, 2007, 4:23pm, ThudanBlunder wrote:
True, but I knew that expert metagrobologists like Eigenray, towr, Grimbal, and SMQ would make short work of them. |
|
I believe that's the first time anyone's used that particular word to describe me.
Incidentally, it seems there's no penury of pentagonal penchants among the pensive. See the penultimate penetration here.
And now I'm more than a little curious about that graph I posted before (I guess there was no reason to hide it). Here's a nicer version (plotting 50000 points). It certainly looks self-similar, so I'm wondering exactly what iterated transformation would give it, or how to try to find it given the data. Is there a closed form for the limit? (At this resolution, it looks exactly the same between 200-201, say.) But I haven't had much time to look into it.
|
| « Last Edit: May 11th, 2007, 5:45pm by Eigenray » |
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
Let p(n) be the probability that a number, picked uniformly from the first n rows of Pascal's triangle, is odd, and let f(x) = 2p(x)*x2-r, where r = log2(3). Then for each x, as k  through integers, f(2kx) converges to some value g(x). The function g satisfies g(2x)=g(x), and for 1<x<2,
g(x) = x-r [ 1+2(x-1)r g(x-1) ].
If (x, y) lies on the graph of g, 1<x<2, then for k=1,2,3,..., so does the point (x', y'), where
x' = 1+x/2k,
y' = x'-r [ 1 + 2(x'-1)r y ].
Starting at a random point and iterating this function system, choosing a random k each time, we get the following picture (in black). The vertical lines are at 1+1/2k, k=1,2,.... Thus the above transformation maps the whole graph into each interval.
Let g0(x)=1, and
gi+1(x) = x-r [ 1 + 2(x-1)r gi(2k(x-1)) ],
where k is the integer such that 1 < 2k(x-1) < 2.
In red, green, and blue, respectively, are shown the graphs of g1, g2, and g3, approximating the graph of g.
The minimum value of g is
 3/[3-2*(2-2)r] = 0.80818...
What is the fractal dimension of this graph?
|
| « Last Edit: May 28th, 2007, 9:47pm by Eigenray » |
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #16 on: Dec 22nd, 2008, 5:08am » |
Quote Modify
|
on May 8th, 2007, 12:39pm, Eigenray wrote:| [How come Firefox and IE treat bgcolor="#252525" as #272A2F?] |
|
They don't, they just think class is more important than background.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #17 on: Dec 22nd, 2008, 6:02am » |
Quote Modify
|
on Dec 22nd, 2008, 5:08am, towr wrote:
They don't, they just think class is more important than background. |
|
Ah, I'll keep that in mind next time I try to hide an image. But then why does .windowbg have background-color #272A2F while the table has bgcolor #252525?
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Triangles, Pentagons, and Hexagons
« Reply #18 on: Dec 22nd, 2008, 6:37am » |
Quote Modify
|
That's just one of those mysteries of life that might only ever be cleared up if William comes round to do so.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print
oddpascal.zip