Author |
Topic: Maximum in every interval (Read 3025 times) |
|
Barukh
Uberpuzzler
Gender: 
Posts: 2276
|
 |
Maximum in every interval
« on: Jun 2nd, 2012, 10:11pm » |
 Quote  Modify
|
Consider a set of records each holding a pair of numerical values (x, y).
Design an efficient dynamic (i.e. with insertions) data structure for the following query: Given a pair x1, x2, return a record with maximal y-value for which x-value lies in the interval [x1, x2].
What is the complexity of insertion and query operations?
|
|
 IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Maximum in every interval
« Reply #1 on: Jun 3rd, 2012, 1:15am » |
Quote Modify
|
You could use a tree, which would be O(log(n)) for queries and insertion.. Store the maximum y for each subtree.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Maximum in every interval
« Reply #2 on: Jun 3rd, 2012, 2:02am » |
Quote Modify
|
Terse, but illuminating 
|
|
IP Logged |
|
|
|
Ela
Newbie
Gender: 
Posts: 25
|
|
Re: Maximum in every interval
« Reply #3 on: Jul 17th, 2012, 2:08am » |
Quote Modify
|
 nice!!
|
|
IP Logged |
|
|
|
sachu
Newbie
Posts: 2
|
|
Re: Maximum in every interval
« Reply #4 on: Jul 25th, 2012, 12:22am » |
Quote Modify
|
I couldn,t understand how the binary tree helps.. Could u please elaborate.....
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
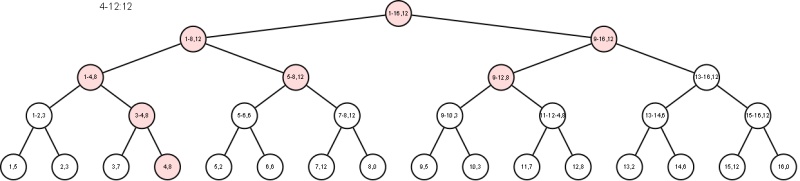
Because each subtree represents a range, you only need to look at a few nodes to find the maximum.
For example in the attachment, the leaf node have x values 1 through 16; each internal node represent a range and contains the maximum in that range. To find the maximum in the range 5-12, you will only need to look at the nodes coloured red to find the maximum. The leaf nodes of the coloured subtree represent the subranges 4, 5-8 and 9-12.
|
| « Last Edit: Jul 25th, 2012, 10:26am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
sachu
Newbie
Posts: 2
|
|
Re: Maximum in every interval
« Reply #6 on: Jul 25th, 2012, 9:56pm » |
Quote Modify
|
gud1....
|
|
IP Logged |
|
|
|
R
Senior Riddler
Addicted!!!
Gender:
Posts: 502
|
|
Re: Maximum in every interval
« Reply #7 on: Sep 14th, 2012, 8:54pm » |
Quote Modify
|
on Jul 25th, 2012, 10:25am, towr wrote:Because each subtree represents a range, you only need to look at a few nodes to find the maximum.
For example in the attachment, the leaf node have x values 1 through 16; each internal node represent a range and contains the maximum in that range. To find the maximum in the range 5-12, you will only need to look at the nodes coloured red to find the maximum. The leaf nodes of the coloured subtree represent the subranges 4, 5-8 and 9-12. |
|
Are you using standard BST or some custom trees to store 'intervals'. I've read somewhere about interval-trees which specifically store (x,y) type of pairs.
|
|
IP Logged |
The first experience seems like Magic, but the second tells you the Trick behind it.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Maximum in every interval
« Reply #8 on: Sep 14th, 2012, 11:42pm » |
Quote Modify
|
A specialized tree would probably be simplest. Otherwise you need to use a custom compare-function or something. But I haven't really considered it at that level of detail.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
R
Senior Riddler
Addicted!!!
Gender:
Posts: 502
|
|
Re: Maximum in every interval
« Reply #9 on: Sep 15th, 2012, 12:55am » |
Quote Modify
|
on Sep 14th, 2012, 11:42pm, towr wrote:| A specialized tree would probably be simplest. Otherwise you need to use a custom compare-function or something. But I haven't really considered it at that level of detail. |
|
Actually I am not able to understand how the tree is being created in your solution. Could you please elaborate more? Thanks.
|
|
IP Logged |
The first experience seems like Magic, but the second tells you the Trick behind it.
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print