Author |
Topic: Hot or cold (Read 8042 times) |
|
Skandh
Junior Member
Gender: 
Posts: 77
|
 |
Hot or cold
« on: Sep 16th, 2011, 8:47am » |
 Quote  Modify
|
Problem Definition goes like this :
Hot or cold. Your goal is the guess a secret integer between 1 and N. You repeatedly guess integers between 1 and N. After each guess you learn if it equals the secret integer (and the game stops); otherwise (starting with the second guess), you learn if the guess is hotter (closer to) or colder (farther from) the secret number than your previous guess. Design an algorithm that finds the secret number in ~ 2 lg N guesses. Then, design an algorithm that finds the secret number in ~ 1 lg N guesses.
I am able to solve first part using Binary Search, but not able to reduce number of guesses to ~ 1 lg N.
Please provide some pointers to proceed with it.
|
|
 IP Logged |
I wanna pull by legs!!!
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Hot or cold
« Reply #1 on: Sep 16th, 2011, 9:35am » |
Quote Modify
|
Just doing binary search seems to work. Start with 1, if N is hotter, then the number lies in (1+N)/2 to N, then if (1+N)/2 is colder, it lies in (N+(1+N))/2 to N, etc. You reduce the search space by a factor of two each step.
|
| « Last Edit: Sep 16th, 2011, 12:25pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Skandh
Junior Member
Gender:
Posts: 77
|
|
Re: Hot or cold
« Reply #2 on: Sep 16th, 2011, 10:18am » |
Quote Modify
|
on Sep 16th, 2011, 9:35am, towr wrote:| Just doing binary search seems to work. Start with 1, if N is hotter, then the number lies in (1+N)/2 to N, then if (1+N)/2 is colder, it lies in (N+(1+N))/2 to N, etc. You reduce the search space by a factor of two each step. |
|
That's correct. But hotter and colder are defined with respect of ( as far as I see it ) older guesses rather than any other number.
if the guess is hotter (closer to) or colder (farther from) the secret number than your previous guess
I'll just elaborate with an example for first part of the question :
Say N=32.
Secret Number = 21
Take mid = 16
First Guess = 8
Second Guess = 24
Since 24 is hotter than 8 so we select interval [17,32]
and so on.
Please correct me if I am wrong.
|
|
IP Logged |
I wanna pull by legs!!!
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Hot or cold
« Reply #3 on: Sep 16th, 2011, 10:28am » |
Quote Modify
|
I'd expect hotter or colder would be with respect to the last guess. So you pick the new number at the opposite end of the range to divide it in two.
So start at 1, then 32, then 16, then 24, then 20, then 22, then 21
|
| « Last Edit: Sep 16th, 2011, 12:25pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Skandh
Junior Member
Gender:
Posts: 77
|
|
Re: Hot or cold
« Reply #4 on: Sep 16th, 2011, 10:35am » |
Quote Modify
|
on Sep 16th, 2011, 10:28am, towr wrote:I'd expect hotter or colder would be with respect to the last guess. So you pick the new number at the opposite end of the range to divide it in two.
So start at 1, then 32, then 16, then 24, then 20, then 22, then 21 |
|
So using this , in worst case, we'll have ~ 2 lg N guesses.
Now how can we decrease number of guesses to ~ 1 lg N?
I just saw hint on book website to decrease number of guesses to ~ 1 lg N, but still not sure how it'll help.
Hint : For the second part, first design an algorithm that solves the problem in ~1 lg N guesses assuming you are permitted to guess integers in the range -N to 2N.
|
|
IP Logged |
I wanna pull by legs!!!
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
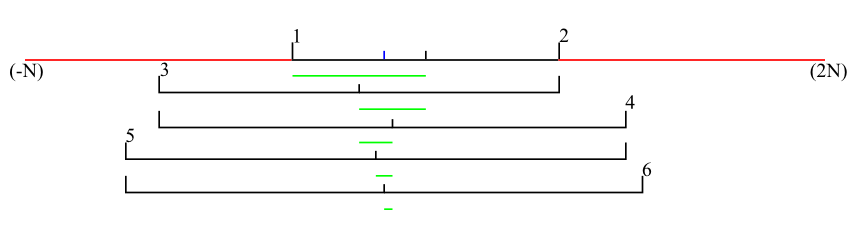
I see now I was just plain wrong in my previous posts.
You want to use the middle between the last point and the next one to have the value you'd use normally for binary search, but to do that you have to pick them outside the range 1-N.
See the attachment for a quick example. Blue is the value you're looking for. The green line shows is your search space. 1,2,3,4,5,6 number the order in which the ends are picked to reduce the search space by halve each step.
|
| « Last Edit: Sep 16th, 2011, 12:50pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print