 Author
Author |
Topic: median in link list (Read 2729 times) |
|
chuncl
Junior Member
 

Gender: 
Posts: 87
|
 |
median in link list
« on: Sep 29th, 2008, 2:58pm » |
 Quote Quote  Modify Modify
|
How to find median in a unsorted single link list efficiently?
I tried to do some search, but found nothing. If it was posted before, I am apologize.
Thanks
|
|
 IP Logged IP Logged |
It is fun
|
|
|
chuncl
Junior Member
 

Gender: 
Posts: 87
|
 |
Re: median in link list
« Reply #2 on: Sep 29th, 2008, 6:06pm » |
 Quote Quote  Modify Modify
|
on Sep 29th, 2008, 4:15pm, Hippo wrote:
thanks, Hippo, yeah, you are right. but then we some time we say that quick sort is not suitable for link-list while merge sort is better? Comments? thanks
|
|
 IP Logged IP Logged |
It is fun
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: median in link list
« Reply #3 on: Sep 30th, 2008, 1:15am » |
 Quote Quote  Modify Modify
|
on Sep 29th, 2008, 6:06pm, chuncl wrote:| thanks, Hippo, yeah, you are right. but then we some time we say that quick sort is not suitable for link-list while merge sort is better? Comments? thanks |
|
Selecting appropriate pivots for quicksort in a list is probably more work.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: median in link list
« Reply #4 on: Sep 30th, 2008, 3:48am » |
 Quote Quote  Modify Modify
|
on Sep 30th, 2008, 1:15am, towr wrote:
Selecting appropriate pivots for quicksort in a list is probably more work.
|
|
No, but the reordering in single linked list causes problems (if you are restricted to use single linked lists during entire algorithm).
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: median in link list
« Reply #5 on: Sep 30th, 2008, 5:37am » |
 Quote Quote  Modify Modify
|
on Sep 30th, 2008, 3:48am, Hippo wrote:| No, but the reordering in single linked list causes problems (if you are restricted to use single linked lists during entire algorithm). |
|
I don't see any reason why you should ever be limited to using just one list. It makes no difference in memory usage to split the list in two during the process (and, if need be, join them at the end).
Finding a random pivot on the other hand can be done in O(1) with a direct access memory structure, but only O(n) in a linked list. (Not that it necessarily needs to be completely random).
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
chuncl
Junior Member
 

Gender: 
Posts: 87
|
 |
Re: median in link list
« Reply #6 on: Sep 30th, 2008, 7:10am » |
 Quote Quote  Modify Modify
|
on Sep 30th, 2008, 5:37am, towr wrote:
I don't see any reason why you should ever be limited to using just one list. It makes no difference in memory usage to split the list in two during the process (and, if need be, join them at the end).
Finding a random pivot on the other hand can be done in O(1) with a direct access memory structure, but only O(n) in a linked list. (Not that it necessarily needs to be completely random). |
|
So for quicksort in single link list,there is no problem in the partition part, the only thing matter here is random selection of pivot? if we don't do random selection of pivot, then quicksort is as applicable to single link list as the merge sort? Is my understanding right? Thanks
|
|
 IP Logged IP Logged |
It is fun
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: median in link list
« Reply #7 on: Sep 30th, 2008, 7:35am » |
 Quote Quote  Modify Modify
|
on Sep 30th, 2008, 7:10am, chuncl wrote:| So for quicksort in single link list,there is no problem in the partition part, the only thing matter here is random selection of pivot? if we don't do random selection of pivot, then quicksort is as applicable to single link list as the merge sort? Is my understanding right? |
|
It is rather critical for quicksort to make a decent selection of the pivot. Otherwise you get quicksort 
And to do that I don't see how you can avoid increasing the cost of pivot selection compared to the case where you have an array.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: median in link list
« Reply #8 on: Sep 30th, 2008, 1:42pm » |
 Quote Quote  Modify Modify
|
The recurence t(n)  2t(n/2)+O(n) gives t(n) 2t(n/2)+O(n) gives t(n)  O(n log n). O(n log n).
Even the recurrence t(n)  t(n1)+t(n2)+O(n) where n1+n2 t(n1)+t(n2)+O(n) where n1+n2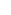 n and n1 n and n1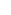 cn cn 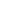 n2 for a constant c gives t(n) n2 for a constant c gives t(n)  O(n log n). O(n log n).
So I cannot see a problem here.
|
| « Last Edit: Sep 30th, 2008, 1:43pm by Hippo » |
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: median in link list
« Reply #9 on: Sep 30th, 2008, 2:06pm » |
 Quote Quote  Modify Modify
|
on Sep 30th, 2008, 1:42pm, Hippo wrote:The recurence t(n)  2t(n/2)+O(n) gives t(n) 2t(n/2)+O(n) gives t(n)  O(n log n). O(n log n).
Even the recurrence t(n)  t(n1)+t(n2)+O(n) where n1+n2 t(n1)+t(n2)+O(n) where n1+n2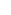 n and n1 n and n1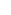 cn cn 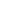 n2 for a constant c gives t(n) n2 for a constant c gives t(n)  O(n log n). O(n log n).
So I cannot see a problem here. |
|
You can't see the problem with having a larger constant factor?
The difference in the constant factor is the whole reason quicksort and heapsort are usually preferred over mergesort in the first place. They're faster, not in an order of magnitude way, but simply in practice.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: median in link list
« Reply #10 on: Sep 30th, 2008, 11:24pm » |
 Quote Quote  Modify Modify
|
Yes, the constant factor grows. I actually do not understand what we are solving now.
If there is single linked list on input and we are allowed to convert the list into an array, we can spend c.n to prepare for standard *sort, and after sorting to convert the array into the single linked list ...
If we are restricted to use single linked list during the entire algorithm, there is no effective implementation of quicksort swap of two elements. OK let we change the quicksort in a way we just split the list into 2(or 3) lists based on comparision with pivot. Even if you do not choose median as a pivot but prefere some sampling, the sampling time is majorized by the list splitting time and it forces much less than doubling the constant factor. The factor grow caused by pointer manipulation would be higher.
On the other side, single linked lists are natural data structures for mergesort.
BTW: Heapsort and Quicksort can sort an array without additional memory ...
|
| « Last Edit: Sep 30th, 2008, 11:26pm by Hippo » |
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: median in link list
« Reply #11 on: Oct 1st, 2008, 12:15am » |
 Quote Quote  Modify Modify
|
on Sep 30th, 2008, 11:24pm, Hippo wrote:| Yes, the constant factor grows. I actually do not understand what we are solving now. |
|
We somehow went from finding the medium to sorting a linked list, I think.
Quote:| OK let we change the quicksort in a way we just split the list into 2(or 3) lists based on comparision with pivot. Even if you do not choose median as a pivot but prefere some sampling, the sampling time is majorized by the list splitting time and it forces much less than doubling the constant factor. The factor grow caused by pointer manipulation would be higher. |
|
What do you mean by "the sampling time is majorized by the list splitting time" ?
It seems to me to find a pivot you'd need to go through half the list on average. So that's a factor of 1.5 (1/2x for finding pivot, 1x for splitting. If pointer manipulation is the largest part of time cost, then that's fairly bad in comparison to mergesort.
Unless we can do them simultaneously (find the next pivots while splitting the list on the current one).
|
| « Last Edit: Oct 1st, 2008, 6:57am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: median in link list
« Reply #12 on: Oct 1st, 2008, 6:06am » |
 Quote Quote  Modify Modify
|
Yes, you translated well what I mean 
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register