 Author
Author |
Topic: Bits in Factorial N (Read 23071 times) |
|
johny_cage
Full Member
  

Gender: 
Posts: 155
|
 |
Bits in Factorial N
« on: Nov 26th, 2007, 5:30am » |
 Quote Quote  Modify Modify
|
Consider the problem of computing N! = 1 . 2 . 3 ... . N
If N is an n-bit number, how many bits long is N!, approximately in terms of theta.
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Bits in Factorial N
« Reply #1 on: Nov 26th, 2007, 8:10am » |
 Quote Quote  Modify Modify
|
If N is a n-bit number, N! is a log2(2n-1!) to log2(2n!) bits long number. 
More seriously, what is theta? (besides the greek letter)
|
| « Last Edit: Nov 26th, 2007, 8:12am by Grimbal » |
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Bits in Factorial N
« Reply #2 on: Nov 26th, 2007, 8:42am » |
 Quote Quote  Modify Modify
|
Theta is pretty much the same as Big O. (See the introduction here.)
Of course, as log(N!) is O(N logN), we have that log(2n!) = O(2nlog(2n)) = O(2n n log2) = O(n 2n).
|
| « Last Edit: Nov 26th, 2007, 8:42am by pex » |
 IP Logged IP Logged |
|
|
|
wanderer
Newbie


Posts: 34
|
 |
Re: Bits in Factorial N
« Reply #3 on: Nov 26th, 2007, 12:15pm » |
 Quote Quote  Modify Modify
|
Or can we analyze like this ?
O(N!) = O(N^N)
and O(N^N) has O(n^2) bits where n is the number of bits in N
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Bits in Factorial N
« Reply #4 on: Nov 26th, 2007, 12:42pm » |
 Quote Quote  Modify Modify
|
Using Stirling's approximation to the factorial, N! 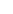  (2 (2 N) NN/eN, so: N) NN/eN, so:
log2(N!) 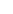 log2((2 log2((2 N)1/2NN/eN) N)1/2NN/eN)
= (1 + log2  + log2 N)/2 + N log2 N - N log2 e + log2 N)/2 + N log2 N - N log2 e
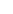 1.326 + n/2 + (n - 1.443)N where n = log2 N. 1.326 + n/2 + (n - 1.443)N where n = log2 N.
--SMQ
|
| « Last Edit: Nov 26th, 2007, 12:45pm by SMQ » |
 IP Logged IP Logged |
--SMQ
|
|
|
johny_cage
Full Member
  

Gender: 
Posts: 155
|
 |
Re: Bits in Factorial N
« Reply #5 on: Nov 27th, 2007, 6:23am » |
 Quote Quote  Modify Modify
|
@All
Plz explain how you are getting this bound????
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register