 Author
Author |
Topic: different ways of expressing the sum of a number. (Read 1112 times) |
|
enabler
Newbie


Gender: 
Posts: 11
|
 |
different ways of expressing the sum of a number.
« on: Jun 18th, 2007, 7:43am » |
 Quote Quote  Modify Modify
|
different ways of expressing the sum of a number.
eg.
for 2
1+1
2
for 3
1+1+1
1+2
2+1
3
please do give algo
|
| « Last Edit: Jun 18th, 2007, 7:45am by enabler » |
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: different ways of expressing the sum of a numb
« Reply #1 on: Jun 18th, 2007, 8:23am » |
 Quote Quote  Modify Modify
|
A search for "partition function" on either Wikipedia or Mathworld should give you several different ways to calculate this.
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: different ways of expressing the sum of a numb
« Reply #2 on: Jun 18th, 2007, 8:23am » |
 Quote Quote  Modify Modify
|
A000041
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: different ways of expressing the sum of a numb
« Reply #3 on: Jun 18th, 2007, 8:36am » |
 Quote Quote  Modify Modify
|
One way would be to find all the partitions of a multiset of n identical elements, then find in how many ways you can arrange the elements of the partition.
e.g
if we have 4
we can have the partitions
{4}
{3,1}
{2,2}
{2,1,1}
{1,1,1,1}
Which you can find quite systematically.
Then find the number of ways to permute the elements from all these multiset partitions.
In this case respectively
1!/1!=1
2!/1!/1! = 2
2!/2!=1
3!/2!/1!=3
4!/4! = 1
which summed gives a total of 8
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: different ways of expressing the sum of a numb
« Reply #4 on: Jun 18th, 2007, 8:40am » |
 Quote Quote  Modify Modify
|
on Jun 18th, 2007, 8:23am, SMQ wrote:| A search for "partition function" on either Wikipedia or Mathworld should give you several different ways to calculate this. |
|
on Jun 18th, 2007, 8:23am, Grimbal wrote:
He's not just asking for the number of partitions though..
I mean, for n=2 he has 2, for n=3 he has 4.
That doesn't exactly match "1, 1, 2, 3, 5, 7, 11, 15 ...", even when shifted.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: different ways of expressing the sum of a numb
« Reply #5 on: Jun 18th, 2007, 8:54am » |
 Quote Quote  Modify Modify
|
on Jun 18th, 2007, 8:40am, towr wrote:| He's not just asking for the number of partitions though.. |
|
Well then it's much simpler: 2n-1. Consider a "list" of n 1's with n-1 symbols inbetween, each of which is either a plus or a comma. Now take the resulting sums for your answers. e.g. for n = 3:
1 , 1 , 1 --> 1 + 1 + 1
1 , 1 + 1 --> 1 + 2
1 + 1 , 1 --> 2 + 1
1 + 1 + 1 --> 3
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
A
Full Member
  

Perder todas as esperanças é liberdade!
Gender: 
Posts: 236
|
 |
Re: different ways of expressing the sum of a numb
« Reply #6 on: Jun 18th, 2007, 9:49am » |
 Quote Quote  Modify Modify
|
As far as i know ,Growth Rate of partition number is ,
partition Number = P(n) = theta((e ^ Pi*(sqrt(2*n/3) )/n)
Code:template <class T> T &min(T& a, T&b){ return a>b?b:a;}
void integerPartitions(int _Remaining, int _UpperBound, int N, vector<int> &_Array)
{
if ( _Remaining == 0 )
{
for ( int ii=1; ii<=N; ii++)
cout << _Array[ii] << "\t"; cout<<endl;
}
else
{
for ( int j=1; j<=min(_UpperBound,_Remaining); j++, _Array)
{
_Array[N+1] = j;
integerPartitions(_Remaining-j, j, N+1,_Array);
}
}
}
void integerPartitions(const int number)
{
vector<int> _Array(number+1,0);
integerPartitions(number, number, 0,_Array);
} |
|
|
|
 IP Logged IP Logged |
What Doesn't Kill Me Will Only Make Me Stronger
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: different ways of expressing the sum of a numb
« Reply #7 on: Jun 18th, 2007, 10:09am » |
 Quote Quote  Modify Modify
|
on Jun 18th, 2007, 8:54am, SMQ wrote:| Well then it's much simpler: 2n-1. |
|
I has that sneaking suspicion when I had the partial sequence 1,2,4,8. But I hadn't worked it out yet.
1's seperated by commas or plusses; very neat.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: different ways of expressing the sum of a numb
« Reply #8 on: Jun 18th, 2007, 1:56pm » |
 Quote Quote  Modify Modify
|
on Jun 18th, 2007, 10:09am, towr wrote:| 1's seperated by commas or plusses; very neat. |
|
Thanks. I suspect there's also a reasonably-natural formulation where 2n-1 arises as the sum of the binomial coefficients of n-1 choose k-1. For instance it's clear that the number of ways to sum to n with exactly two numbers is n-1 choose 1 -- pick the first number of the pair from 1...n-1 , and the other is forced. It's less clear that the number of ways to sum to n with exactly three numbers is n-1 choose 2 -- or in general that the number of ways to sum to n with exactly k numbers is n-1 choose k-1 -- but it "feels right," and some quick examples seem to bear it out...
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: different ways of expressing the sum of a numb
« Reply #9 on: Jun 19th, 2007, 9:38am » |
 Quote Quote  Modify Modify
|
on Jun 18th, 2007, 1:56pm, SMQ wrote:
<snip>
It's less clear that the number of ways to sum to n with exactly three numbers is n-1 choose 2 --
<snip>
--SMQ |
|
Using your own idea  Ditch the plusses and use 2 commas and interpret the numbers in base 1. Ditch the plusses and use 2 commas and interpret the numbers in base 1.
|
| « Last Edit: Jun 19th, 2007, 9:38am by Aryabhatta » |
 IP Logged IP Logged |
|
|
|
enabler
Newbie


Gender: 
Posts: 11
|
 |
Re: different ways of expressing the sum of a numb
« Reply #10 on: Jun 21st, 2007, 12:40am » |
 Quote Quote  Modify Modify
|
My question was if a number is given as input.....
It should print its different ways of expressing its SUM.
input : 2
output:
1 1
2
input : 3
1 1 1
1 2
2 1
3
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: different ways of expressing the sum of a numb
« Reply #11 on: Jun 21st, 2007, 12:52am » |
 Quote Quote  Modify Modify
|
on Jun 21st, 2007, 12:40am, enabler wrote:My question was if a number is given as input.....
It should print its different ways of expressing its SUM. |
|
Ah, I thought you only wanted the number of ways.
But, unless you also want them in a particular order, SMQs solution gives an easy way to give the various representations.
Just take all binary numbers up to 2n-1, imagine a 0 in front and after it. Take the number of set bits between each two consecutive 0's, add 1 to each, print as sum
so e.g. 1101110010 -> 011011100100 -> {2,3,0,1,0} -> {3,4,1,2,1} -> print(3+4+1+2+1)
|
| « Last Edit: Jun 25th, 2007, 5:14am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: different ways of expressing the sum of a numb
« Reply #12 on: Jun 21st, 2007, 6:48am » |
 Quote Quote  Modify Modify
|
in C++:
void printSums(unsigned int n) {
if (n < 1 || n > 32) {
cerr << "error: n must be from 1 to 32" << endl;
return;
}
for(unsigned long i = 0; i < (1UL << (n-1)); i++) {
unsigned int x = 1;
for(unsigned int j = 0; j < (n-1); j++) {
if ((i & (1UL << j)) != 0) {
cout << x << " ";
x = 1;
} else {
x++;
}
}
cout << x << endl;
}
}
--SMQ
|
| « Last Edit: Jun 21st, 2007, 7:11am by SMQ » |
 IP Logged IP Logged |
--SMQ
|
|
|
enabler
Newbie


Gender: 
Posts: 11
|
 |
Re: different ways of expressing the sum of a numb
« Reply #13 on: Jun 22nd, 2007, 3:11am » |
 Quote Quote  Modify Modify
|
this works well but it consumes O(n) space
but there is more efficient solution than this............
#include<stdio.h>
#include<conio.h>
#include<stdlib.h>
void sum(int a[],int left,int right)
{
if(left<right)
{
printf("\n");
for(int i=left;i<=right;i++)
printf("%d ",a[i]);
if(a[left+1]==1)
{
a[left+1]=a[left]+1;
sum(a,left+1,right);
a[left+1]=a[left+1]-a[left];
}
if(a[right-1]==1)
{
a[right-1]=a[right]+1;
sum(a,left,right-1);
a[right-1]=a[right-1]-a[right];
}
}
}
int main()
{
int N=3;
clrscr();
int *p=(int*)malloc(sizeof(int)*N);
for(int i=0;i<N;i++)
p[i]=1;
sum(p,0,N-1);
getch();
return 1;
}
|
|
 IP Logged IP Logged |
|
|
|
sumantbhardvaj
Newbie


Posts: 20
|
 |
Re: different ways of expressing the sum of a numb
« Reply #14 on: Jun 25th, 2007, 4:53am » |
 Quote Quote  Modify Modify
|
I could not fully grasp the code implemented by SMQ.
Can any body explain how's that working ?
Does that code implement the same method suggested by towr above...
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: different ways of expressing the sum of a numb
« Reply #15 on: Jun 26th, 2007, 7:01am » |
 Quote Quote  Modify Modify
|
on Jun 25th, 2007, 4:53am, sumantbhardvaj wrote:| Can any body explain how's that working ? |
|
Certainly!
Theory:
The question asks for all the sums of positive integers totaling a given value 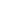 . This can be restated as listing all partitions of an ordered list of . This can be restated as listing all partitions of an ordered list of 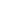 elements. That is, given positive integers elements. That is, given positive integers 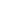 1, 1, 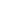 2, ... 2, ... 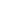  such that such that   =1 =1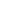 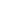  = = 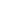 , the first partition contains elements 1 through , the first partition contains elements 1 through 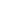 1, the second partition contains elements 1, the second partition contains elements 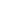 1+1 through 1+1 through 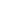 1+ 1+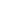 2, etc., with the 2, etc., with the  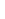  partition containing elements ( partition containing elements (  =1 =1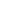   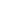  )+1 through )+1 through 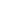 . Now the list of such partitions is simple to generate: consider, for each 1 . Now the list of such partitions is simple to generate: consider, for each 1   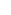 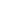 , whether or not the list is partitioned after the , whether or not the list is partitioned after the  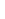  element. There are clearly 2 element. There are clearly 2   unique partitionings, and thus 2 unique partitionings, and thus 2   unique sums in the original problem statement. unique sums in the original problem statement.
Implementation:
First, a quick check to be sure that the given value of n is reasonable. If n = 0 then there are no results; if n > 32 then the simple bit-counting algorithm below will fail (but since n = 32 already generates upwards of 2 billion results, listing all possible sums for such n is impractical anyway).
Next, we let the index variable i loop from 0 to 2n-1-1 (note that 1 << m = 2m). Each partitioning is thus associated with a value of i by the bits of i: the list is partitioned after element  if and only if bit if and only if bit  - 1 (0-based) of i is 1. - 1 (0-based) of i is 1.
Within the outer loop, we establish x as an accumulator to convert from a partitioning to the original problem statement: x counts the number of elements in the current partition. Now we use the loop index j to loop over the bits of i. (Note that because the LSB of i is bit 0, j runs from 0 to n - 2 rather than from 1 to 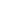 - 1 as given in the Theory section.) - 1 as given in the Theory section.)
If the jth bit of i is set (i & 2j  0), the list is partitioned after the j + 1st element: output the current value of the accumulator, x, and reset it to 1. Otherwise, the list is not partitioned after element j + 1; just increment the accumulator. 0), the list is partitioned after the j + 1st element: output the current value of the accumulator, x, and reset it to 1. Otherwise, the list is not partitioned after element j + 1; just increment the accumulator.
Last, after checking all n - 1 bits of i, output the final value of the accumulator x.
Hope that makes things clear!
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
findmeeifucan
Newbie


Gender: 
Posts: 2
|
 |
Re: different ways of expressing the sum of a numb
« Reply #16 on: Jul 14th, 2007, 6:48am » |
 Quote Quote  Modify Modify
|
The sum
2+2
repeated twice for input 4 when number of ways is taken as 2^n-1. Is 2^n-1 is correct answer or it should be all the non repeated ways of describing sum.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: different ways of expressing the sum of a numb
« Reply #17 on: Jul 15th, 2007, 9:12am » |
 Quote Quote  Modify Modify
|
on Jul 14th, 2007, 6:48am, findmeeifucan wrote:The sum
2+2
repeated twice for input 4 when number of ways is taken as 2^n-1. Is 2^n-1 is correct answer or it should be all the non repeated ways of describing sum. |
|
It wouldn't be repeated twice in the 2^(n-1) count; the parenthesis are important though.
4
3+1
2+2
1+3
2+1+1
1+2+1
1+1+2
1+1+1+1
2^(4-1)=8, fits exactly.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register