Author |
Topic: Facebook Puzzles (Read 3198 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Facebook Puzzles
« on: Apr 30th, 2007, 9:51am » |
 Quote  Modify
|
Thought you might like these.
|
|
 IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
A
Full Member
Perder todas as esperanças é liberdade!
Gender:
Posts: 236
|
|
Re: Facebook Puzzles
« Reply #1 on: May 7th, 2007, 8:10am » |
Quote Modify
|
i wonder if we can do 'Prime Bits" puzzle in better than O(M Log N) time ?
M::number of integers between a and b
N::number of bits used to represent integers 
|
|
IP Logged |
What Doesn't Kill Me Will Only Make Me Stronger
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Facebook Puzzles
« Reply #2 on: May 7th, 2007, 8:23am » |
Quote Modify
|
on May 7th, 2007, 8:10am, R0B1N wrote:i wonder if we can do 'Prime Bits" puzzle in better than O(M Log N) time ?
M::number of integers between a and b
N::number of bits used to represent integers |
|
I think you probably can, although I'm not entirely sure yet how.
If a-1 and b are powers of two, I can see a fairly easy way to get the answer though. Possibly it can be extended for the general case.
Say b is 2k, then you want the sum of the number of (unique) permutations of p 1-bits and k-p 0-bits over all prime p <= k. This is simple enough to calculate.
|
| « Last Edit: May 7th, 2007, 8:23am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Facebook Puzzles
« Reply #3 on: May 7th, 2007, 2:52pm » |
Quote Modify
|
I'm sure it's polynomial in the number of bits k.
| hidden: | For each prime p <= k, find A and B, the smallest numbers greater than or equal to a and (b+1), respectively, which have exactly p bits set (B might not exist, but that's easy to handle). To do this, if a has t < p bits set, just flip the rightmost p-t 0s of a to get A. And if t > p, find the rightmost 0 to the left of the rightmost (t-p+1) 1s, make it a 1, clear everything to the right, and then add the appropriate number of 1s (from the right).
Now just increment the count by r(B) - r(A), where r(A) is the lexicographic rank of A as a p-set. Compute r recursively: if A = 2s + A', where A' < 2s, then rp(A) = C(s,p) + rp-1(A'). |
|
| « Last Edit: May 7th, 2007, 3:02pm by Eigenray » |
IP Logged |
|
|
|
jesse
Newbie
Posts: 2
|
|
Re: Facebook Puzzles
« Reply #4 on: May 8th, 2007, 5:40pm » |
Quote Modify
|
Hey everyone. I stumbled across this forum and thought I'd share my solutions to two of the puzzles ("Prime Bits" and "Korn Shell"). Facebook asked me to obscure the solutions -- I used to have all the code posted publicly -- but the reasoning is still all three.
Only go there if you want the solutions.
Cheers, and let me know what you think.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Facebook Puzzles
« Reply #5 on: May 9th, 2007, 12:32am » |
Quote Modify
|
on May 8th, 2007, 5:40pm, jesse wrote:| Hey everyone. I stumbled across this forum and thought I'd share my solutions to two of the puzzles ("Prime Bits" and "Korn Shell"). Facebook asked me to obscure the solutions -- I used to have all the code posted publicly -- but the reasoning is still all there. |
|
For the two-character case of "Korn Shell", you wrote down 3 cycles where it ought to be just 11 and 15 (rather than 3, 5 and 11)
A nice and clear write-up of the solution though.
It might be fun to use template meta-programming in C++ to give a solution. You'd be able to calculate all the cases at compile time (rather than doing it in a seperate program beforehand) and still return answers in optimal run-time. Although I wouldn't claim it's easy 
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
jesse
Newbie
Posts: 2
|
|
Re: Facebook Puzzles
« Reply #6 on: May 9th, 2007, 10:07am » |
Quote Modify
|
Oops, yes. I got 165 and then just blindly wrote down the prime factors.
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Facebook Puzzles
« Reply #7 on: May 10th, 2007, 3:23am » |
Quote Modify
|
Jesse, I liked very much your analysis of the "Prime Bits" problem.
Well done! 
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Facebook Puzzles
« Reply #8 on: May 13th, 2007, 3:31am » |
Quote Modify
|
For any n, estimate the number of "Prime Bits" numbers in the range [1, 2n].
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
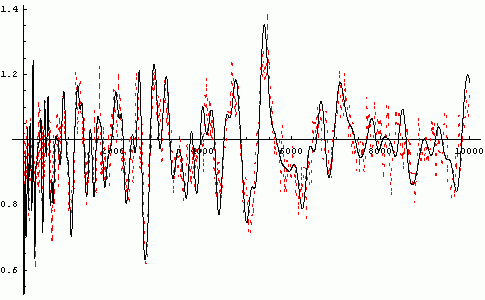
Let f(n) = the number of prime-bit numbers between 1 and 2n.
Here's f(n)/[2n/log(n/2)].
The dashed red line is based on a sampling of [ (n/2+ n) - (n/2-n)]/[2n / log(n/2)], where (n) is the prime counting function.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print