Author |
Topic: onto function (Read 3973 times) |
|
guitar
Newbie
Posts: 1
|
 |
onto function
« on: Feb 6th, 2007, 10:03am » |
 Quote  Modify
|
how do you provethe number of onto functions. How many onto functions are there.
|
|
 IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: onto function
« Reply #1 on: Feb 6th, 2007, 11:21am » |
Quote Modify
|
Well, each element in the range needs at least one element in the domain to map to it, and the rest can be distributed arbitrarily.
I'm gonna go with |D|!/[(|D|-|R|)! * |R|!] * |R|(|D|-|R|) for now. But I might be wrong, it's tricky to choose the right distribution scheme.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
shishir85
Newbie
 
Gender:
Posts: 19
|
|
Re: onto function
« Reply #2 on: Feb 6th, 2007, 10:21pm » |
Quote Modify
|
Can I rephrase this question as:
There are 'R' buckets numbered 1 to R. There are 'D' balls numbered 1 to D. D >= R. These balls have to be put in the buckets such that each bucket should get atleast one ball. Find the number of ways to do this?
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: onto function
« Reply #3 on: Feb 7th, 2007, 12:31am » |
Quote Modify
|
on Feb 6th, 2007, 10:21pm, shishir85 wrote:Can I rephrase this question as:
There are 'R' buckets numbered 1 to R. There are 'D' balls numbered 1 to D. D >= R. These balls have to be put in the buckets such that each bucket should get atleast one ball. Find the number of ways to do this? |
|
That was how I interpreted it, at least.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
shishir85
Newbie
Gender:
Posts: 19
|
|
Re: onto function
« Reply #4 on: Feb 7th, 2007, 9:36am » |
Quote Modify
|
on Feb 7th, 2007, 12:31am, towr wrote:
That was how I interpreted it, at least.
|
|
hmm..towr I think your solution will not work. Take R=1 (ie just one bucket). There is only one way to put all the balls. But your solution will give answer: D.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: onto function
« Reply #5 on: Feb 7th, 2007, 10:41am » |
Quote Modify
|
on Feb 7th, 2007, 9:36am, shishir85 wrote:hmm..towr I think your solution will not work. Take R=1 (ie just one bucket). There is only one way to put all the balls. But your solution will give answer: D.
|
|
Hmm, |D|, yes.. Well, that's wrong then!
Time to rethink it.. I don't suppose you have a suggestion?
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: onto function
« Reply #6 on: Feb 7th, 2007, 8:54pm » |
Quote Modify
|
The number of functions f : D -> R whose image is contained in some set S is just |S|d, where d=|D|, r=|R|. So we can use inclusion-exclusion to get that the number of functions whose image is exactly R is
[sum]{S c R} (-1)|R\S| |S|d
= [sum]k=0r C(r,k) (-1)r-k kd,
since there are C(r,k) subsets S 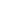 R with |S|=k. That's about as "closed form" as you're gonna get, but this number is important enough to have its own name. An onto function f can be thought of as partitioning D into the |R| non-empty subsets f-1(y) = {x : f(x)=y}, and conversely such a partition of D into |R| (ordered) non-empty subsets uniquely determines f. So the number of onto functions is given by
r! S(d,r),
where (by definition) S(d,r) is the number of ways to partition a d-element set into r non-empty subsets (since there are r! possible ways to order the r sets).
This is but one case of the Twelvefold way.
|
|
IP Logged |
|
|
|
shishir85
Newbie
Gender:
Posts: 19
|
|
Re: onto function
« Reply #7 on: Feb 7th, 2007, 9:52pm » |
Quote Modify
|
Let r = |R| and d = |D|.
1. The total number of functions possible = rd.
From this we have to subtract the number of functions which are not onto.
2. When exactly one element in R is left out (ie not mapped to), number of possible functions is: (r-1)d. Also there are C(r,1) ways to select the element in R which is left out.
3. Similarly, when exactly 'k' elements in R are left out (ie not mapped to), number of possible functions is : (r-k)d. Also there are C(r,k) ways to select the elements in R which are left out.
So, final answer should be:
rd - [sum]k=1 to r-1 C(r,k)(r-k)d
|
| « Last Edit: Feb 7th, 2007, 9:53pm by shishir85 » |
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: onto function
« Reply #8 on: Feb 8th, 2007, 4:23am » |
Quote Modify
|
A recursion to calculate the numbers
T(d, d) = 1
T(d, 1) = 1
T(d, r) = r * [ T(d - 1, r - 1) + T(d - 1, r) ]
http://www.research.att.com/~njas/sequences/A019538
And I suppose that's sufficiently beating this horse to death 
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
shishir85
Newbie
Gender:
Posts: 19
|
|
Re: onto function
« Reply #9 on: Feb 8th, 2007, 5:54am » |
Quote Modify
|
on Feb 8th, 2007, 4:23am, towr wrote:
Why is T(d,d) = 1?
I think it should be d! ( d factorial).
When I rephrased the problem in terms of balls and buckets, both balls and buckets were numbered. That means, no two buckets are similar and also no two balls are similar. T(d,d) will be 1 when balls and buckets are not numbered (so, there is no way to differentiate between any two balls or any two buckets). In that case, it does not matter which ball goes into which bucket as long as all the buckets have atleast one ball.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: onto function
« Reply #10 on: Feb 8th, 2007, 9:44am » |
Quote Modify
|
on Feb 8th, 2007, 5:54am, shishir85 wrote:Why is T(d,d) = 1?
I think it should be d! ( d factorial). |
|
Err, yes.. Small error adapting the recursion for stirling numbers of the second kind..
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print