Author |
Topic: conformal mapping (Read 8214 times) |
|
trusure
Newbie
Gender: 
Posts: 24
|
 |
conformal mapping
« on: Apr 19th, 2009, 9:52am » |
 Quote  Modify
|
I'm trying to construct a conformal map from
D(0,1)\[a,1) to D(0,1) , where 0<a<1 , but it didn't work with me!
if it is from D(0,1) to D(0,1) it is easy, but here ??!
can anyone help me, actually,I have a problem with understanding how I can construct such mapping !?
Thank you
|
|
 IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender: 
Posts: 1948
|
|
Re: conformal mapping
« Reply #1 on: Apr 19th, 2009, 6:40pm » |
Quote Modify
|
The map z 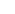 i(1-z)/(1+z) takes the disk to the upper-half plane, and the slit [a,1) to the slit (0, (1-a)/(1+a)i ]. For simplicity scale so that the slit becomes (0, i].
Now we basically have a polygonal region so we can use a Schwarz-Christoffel integral, with vertices at 0, i, and 0, and interior angles  /2, 2, and /2, respectively, to map the upper-half plane to this region.
F(z) = i +  0z w dw/[(w-1)1/2 (w+1)1/2]
does the trick (taking the branch of sqrt which is positive on the positive real axis).
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print