 Author
Author |
Topic: conformal mapping problem (Read 14623 times) |
|
immanuel78
Newbie



Gender: 
Posts: 23
|
 |
conformal mapping problem
« on: Feb 11th, 2009, 6:21am » |
 Quote Quote  Modify Modify
|
Show that there is an analytic function defined on G=ann(0;0;1) such that f'(prime) never vanishes and f(G)=B(0;1).
This problem comes from the textbook by John. Conway-In particular, Riemann mapping theorem
section.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: conformal mapping problem
« Reply #1 on: Feb 11th, 2009, 5:17pm » |
 Quote Quote  Modify Modify
|
That's a good question.
If we didn't require f to be locally injective we could simply take an automorphism of the unit disk  that moves 0, and then compose with squaring. that moves 0, and then compose with squaring.
By the Riemann mapping theorem, it suffices to show that there is a surjective conformal map from X \ {p} to Y, where X,Y are proper simply connected domains, and p  X. Then you can compose with the biholomorphic maps between X,Y, and X. Then you can compose with the biholomorphic maps between X,Y, and  , and an automorphism taking 0 to the appropriate point. , and an automorphism taking 0 to the appropriate point.
In fact we can replace  \ {p} with \ {p} with  \ {p1,...,pn}, where n \ {p1,...,pn}, where n  1. That is, for any p1,...,pn 1. That is, for any p1,...,pn   , we can find q1,...,qn-1 , we can find q1,...,qn-1   and a surjective conformal map from and a surjective conformal map from  \ {q1,...,qn-1} to \ {q1,...,qn-1} to  \ {p1,...,pn}. To see this, apply an automorphism to take pn = 0, and pick J an interval of length > 2 \ {p1,...,pn}. To see this, apply an automorphism to take pn = 0, and pick J an interval of length > 2 which contains exactly one argument of each of p1,...,pn-1. Then exp takes U = { x + i y | x < 0, y which contains exactly one argument of each of p1,...,pn-1. Then exp takes U = { x + i y | x < 0, y  J } surjectively onto J } surjectively onto  \ {0}, and we just remove the preimages of p1,...,pn-1. \ {0}, and we just remove the preimages of p1,...,pn-1.
The simplest example I can think of is to take X a large disk around the origin, and f(z) = z2(z-1). We need to remove {0, 2/3} since these are the points where f'(z)=0. But f(1) = f(0) and f(-1/3) = f(2/3), so as long as X is big enough, f(X \ {0,2/3}) = f(X).
It remains to show that for X large enough, f(X) is simply connected. Actually I'm not sure how to do this, but it should be true for any polynomial.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: conformal mapping problem
« Reply #2 on: Feb 12th, 2009, 3:20am » |
 Quote Quote  Modify Modify
|
Maybe this is easier:
Let  (z) = z+1/z, and for r > 1, let Ar = { z : 1/r < |z| < r }. Then (z) = z+1/z, and for r > 1, let Ar = { z : 1/r < |z| < r }. Then  (Ar) is the interior of the ellipse (x/(r+1/r))2 + (y/(r-1/r))2 = 1. In particular, it is simply connected. (Ar) is the interior of the ellipse (x/(r+1/r))2 + (y/(r-1/r))2 = 1. In particular, it is simply connected.
Now, let F(z) = z3 - 3z. Since F( (z)) = (z)) =  (z3), F( (z3), F( (Ar)) = (Ar)) =  (Ar^3) is also simply connected. (Ar^3) is also simply connected.
F is conformal on  (Ar), except at z = (Ar), except at z =  1. But we can remove these points without changing the image because F( 1. But we can remove these points without changing the image because F( 2) = F( 2) = F( 1). 1).
To sum up:
(disk minus a point) 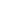 (half-strip minus a point) (half-strip minus a point) 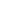 (disk minus 2 points) (disk minus 2 points) 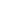 ( ( (Ar) \ { (Ar) \ { 1}) 1}) 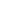  (Ar^3) (Ar^3) 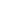 disk, disk,
where the 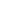 maps are exp and F, respectively. maps are exp and F, respectively.
|
| « Last Edit: Feb 12th, 2009, 3:43am by Eigenray » |
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: conformal mapping problem
« Reply #3 on: Feb 15th, 2009, 10:09am » |
 Quote Quote  Modify Modify
|
Clever example! How did you come with it?
I have done a similar thing to produce a locally
univalent but not univalent holomorphic map of
the unit disk onto a convex image. You should be
able to see how to do that from what you did
here.
|
| « Last Edit: Feb 15th, 2009, 10:18am by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: conformal mapping problem
« Reply #4 on: Feb 15th, 2009, 10:49am » |
 Quote Quote  Modify Modify
|
I had the same idea: try to find a non-injective conformal map between two simply connected regions. The exponential won't work (since the image of a path between z and z + 2 i k has winding number k), so I thought about taking a polynomial and removing the roots of the derivative, since we can add as many holes as we want. A quadratic won't work, so I tried a cubic. I wasn't sure how to show the image was simply connected though so I checked the section of Ahlfors on conformal mappings, where he uses the trick of pulling back via z = w+1/w to reduce a general cubic to w i k has winding number k), so I thought about taking a polynomial and removing the roots of the derivative, since we can add as many holes as we want. A quadratic won't work, so I tried a cubic. I wasn't sure how to show the image was simply connected though so I checked the section of Ahlfors on conformal mappings, where he uses the trick of pulling back via z = w+1/w to reduce a general cubic to w 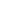 w3. w3.
|
| « Last Edit: Feb 15th, 2009, 10:55am by Eigenray » |
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: conformal mapping problem
« Reply #5 on: Feb 18th, 2009, 8:31am » |
 Quote Quote  Modify Modify
|
Thanks.
For some a, 0 < a < 1 , then z(z^2 - a^2)/(a^2 z^2 - 1) maps D
onto D and branches at exactly two points z1,z2 . (D \ {z1,z2}) maps
to the unit disk. We can get a conformal map from D onto D by considering
a composed universal covering map of the domain. Now just restrict
the domain to the annulus.
|
| « Last Edit: Feb 18th, 2009, 8:48am by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: conformal mapping problem
« Reply #6 on: Mar 9th, 2009, 6:46pm » |
 Quote Quote  Modify Modify
|
Here are some similar constructions to yours:
1. D.S.Greenstein, Monthly 65 ( 1958 ) , p.214.
2. Due to John V.Ryff (in a totally inaccessible 1969
journal (Math Reviews, vol. 42, review #1981.
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register