 Author
Author |
Topic: Analytic problem (Read 10106 times) |
|
Felix.R
Newbie


Posts: 7
|
 |
Analytic problem
« on: Jun 12th, 2007, 2:32pm » |
 Quote Quote  Modify Modify
|
Suppose g is analytic on abs(z)<=1 and let abs(g(z)) be maximized for abs(z)<=1 at z0 with abs(z0)=1. Prove that g'(z0) is not zero unless g is constant.
|
|
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Analytic problem
« Reply #1 on: Jun 13th, 2007, 9:52am » |
 Quote Quote  Modify Modify
|
You should be able to solve this using Schwarz. Notice that
|g(z)| < 1 in |z| < 1 by the maximum principle.
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Felix.R
Newbie


Posts: 7
|
 |
Re: Analytic problem
« Reply #2 on: Jun 15th, 2007, 10:51pm » |
 Quote Quote  Modify Modify
|
Is it because the function g is not constant that the maximum principle gives the statement you made? Actually this is not that easy to see for one thing. I think. I am not sure what to do with Schwarz's lemma because it does not appear to lead me to a function composed with g that I can work with. So I don't understand how I can solve it using Schwarz. Explain if you will.
|
|
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Analytic problem
« Reply #3 on: Jun 17th, 2007, 8:57pm » |
 Quote Quote  Modify Modify
|
Yes. You are at liberty to make some assumptions here.
For example, you may assume that g(z0) = z0, z0 = 1.
Noting that |g(z)| < 1 in |z| < 1, and so if we take
g(0) = 0 then by Schwarz we have |g(z)| <= |z|, |z| < 1.
|
| « Last Edit: Jun 17th, 2007, 9:00pm by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Felix.R
Newbie


Posts: 7
|
 |
Re: Analytic problem
« Reply #4 on: Jun 18th, 2007, 6:36pm » |
 Quote Quote  Modify Modify
|
I do not follow all this. I understand assuming g(1) = 1 and g(0) = 0 but doesn't this require that we also assume that g(0) not zero? Also, I can't use the bar character for absolute value I guess because my language pack seems to display character codes on this web site for that symbol. I have no idea why.
|
| « Last Edit: Jun 18th, 2007, 6:37pm by Felix.R » |
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Analytic problem
« Reply #5 on: Jun 18th, 2007, 7:07pm » |
 Quote Quote  Modify Modify
|
I just lost a fair amount of typed text here. I am
certainly annoyed by expired pages messages.
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Analytic problem
« Reply #6 on: Jul 10th, 2007, 9:58am » |
 Quote Quote  Modify Modify
|
Did you solve this problem?
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Felix.R
Newbie


Posts: 7
|
 |
Re: Analytic problem
« Reply #7 on: Jul 11th, 2007, 9:32am » |
 Quote Quote  Modify Modify
|
Alas, only partially to a degree with some missing pieces using a Taylor series. We appreciate help!
|
|
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Analytic problem
« Reply #8 on: Jul 30th, 2007, 6:56pm » |
 Quote Quote  Modify Modify
|
That leads me to guess what you mean but you might be
on to something. Is that series that of g(z) - g(z0) ?
See what you can do with this:
Show that |g'(1)| >= 1 and take g(0) = a, a <> 0. Now
consider
h(z) = (g(z) - a)/(1 - a bar g(z)).
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Analytic problem
« Reply #9 on: Sep 15th, 2007, 8:34am » |
 Quote Quote  Modify Modify
|
Did you try to work with this?
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Analytic problem
« Reply #10 on: Sep 29th, 2007, 7:16pm » |
 Quote Quote  Modify Modify
|
What happened to you on this problem?
This is a nice problem by the way -- not too hard
but interesting, but maybe you solved it and
forgot about us?
I would like to see what you came up with.
|
| « Last Edit: Sep 29th, 2007, 7:30pm by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Analytic problem
« Reply #11 on: Sep 29th, 2007, 7:21pm » |
 Quote Quote  Modify Modify
|
Yea seems like he is MIA..
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Ghost Sniper
Senior Riddler
   

Do not hide. It is useless.
Gender: 
Posts: 599
|
 |
Re: Analytic problem
« Reply #12 on: Dec 13th, 2007, 10:51am » |
 Quote Quote  Modify Modify
|
[redacted] im right
// excuse me? --SMQ
|
| « Last Edit: Dec 13th, 2007, 11:06am by SMQ » |
 IP Logged IP Logged |
*sob* I miss my mommy... *blows nose* huh, I'm on? oh right.
(thinks to self) Time for my speech to these college kids.
"Reason is more important than all emotions..."
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Analytic problem
« Reply #13 on: Jan 23rd, 2008, 11:35pm » |
 Quote Quote  Modify Modify
|
>> [redacted] im right
>> excuse me? --SMQ
Being curious, I had wondered what this exchanged
was referring to but apparently I had miss it at some
point -- perhaps Ghost had proposed solution but
took it back (?).
Still, a pretty cool problem, and in spite of my remarks it has
gone unsolved -- on this forum nevertheless.
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Analytic problem
« Reply #14 on: Mar 14th, 2008, 6:43pm » |
 Quote Quote  Modify Modify
|
I don't think you need anything but the power series expansion. We can assume z0=1, and g(1)=1 (if g is not identically 0). Then for some n  1, 1,
g(1+w) - 1 = wn (C + O(w)),
where C = g(n)(1)/n!  0. Writing w=reit, then for t fixed, 0. Writing w=reit, then for t fixed,
Arg [ g(1+w) - 1 ]  nt + Arg[C] nt + Arg[C]
as r  0. If n 0. If n  2, then for some integer k, we can take t = (2 2, then for some integer k, we can take t = (2 k-Arg[C])/n k-Arg[C])/n  ( ( /2, 3 /2, 3 /2). Then Arg[g(1+w)-1] /2). Then Arg[g(1+w)-1]  0, and therefore for r sufficiently small, |g(1+w)| > 1, with 1+w in the unit disk. 0, and therefore for r sufficiently small, |g(1+w)| > 1, with 1+w in the unit disk.
|
|
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Analytic problem
« Reply #15 on: Mar 21st, 2008, 1:59pm » |
 Quote Quote  Modify Modify
|
Geometrically nice!
I think your proof could be made to show that the
derivative at 1 is actually positive (not just non-zero)!
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Analytic problem
« Reply #16 on: Mar 21st, 2008, 2:50pm » |
 Quote Quote  Modify Modify
|
Actually, we can think of it like a Lagrange multiplier problem:
 |f|2(z0) = |f|2(z0) =  z0 for some z0 for some   0, 0,
since otherwise we could increase |f| by moving along the unit circle (or in the -z0 direction, if  < 0). Since < 0). Since
 |f|2 = 2f bar[f'], |f|2 = 2f bar[f'],
we get that
f'(z0) = t z0/bar[f(z0)]
for some t  0, but we need analycity (analyticality?) of f to get t 0, but we need analycity (analyticality?) of f to get t  0. 0.
|
|
 IP Logged IP Logged |
|
|
|
TJMann
Newbie


Posts: 18
|
 |
Re: Analytic problem
« Reply #17 on: Mar 22nd, 2008, 11:49pm » |
 Quote Quote  Modify Modify
|
Pardon, but how is  |f|2(z0) read? I have never seen del used with complex functions before. Also, I thought analyticity is pre-supposed if you write f'(z)? |f|2(z0) read? I have never seen del used with complex functions before. Also, I thought analyticity is pre-supposed if you write f'(z)?
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Analytic problem
« Reply #18 on: Mar 23rd, 2008, 12:40am » |
 Quote Quote  Modify Modify
|
I'm thinking of h(x,y) = |f(x+iy)|2 = u2 + v2 just as a real-valued function of two real variables. Then  h is a vector in h is a vector in  2, which I'm thinking of as the complex number 2, which I'm thinking of as the complex number
 h = h = 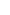 h/ h/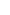 x + i x + i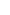 h/ h/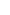 y y
= (2uux+2vvx) + i(2uuy+2vvy)
= 2(u+iv)(ux+iuy)
= 2f bar[f'],
using ux=vy, uy=-vx. We could also compute
hz = (f bar f)z
= fz (bar f) + f (bar f)z
= f' * bar f,
since bar f is antiholomorphic, and use the fact that  h = 2 bar[hz]. I don't know if this is standard notation, though. h = 2 bar[hz]. I don't know if this is standard notation, though.
My point was just that from the point of view of multivariable calculus, it's clear that  h must be perpendicular to the unit circle, but it's not clear that it can't be the zero vector. That is where we need to think of f as a complex analytic function, not just as a function from h must be perpendicular to the unit circle, but it's not clear that it can't be the zero vector. That is where we need to think of f as a complex analytic function, not just as a function from  2 2   2. 2.
|
| « Last Edit: Mar 23rd, 2008, 12:40am by Eigenray » |
 IP Logged IP Logged |
|
|
|
TJMann
Newbie


Posts: 18
|
 |
Re: Analytic problem
« Reply #19 on: Mar 24th, 2008, 9:59am » |
 Quote Quote  Modify Modify
|
cool. I never thought of it like that and saves lots of space. In your last paragraph, I don't see why the gradient of h is perpendicular to the unit circle though, I think to the level lines of h it is, {(x,y), h(x,y) = const}
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Analytic problem
« Reply #20 on: Mar 24th, 2008, 1:56pm » |
 Quote Quote  Modify Modify
|
This is just because  h points in the direction of increasing h. Let v be a unit vector tangent to the unit circle at z0. Then the directional derivative of h in the direction v is just Dv h = < h points in the direction of increasing h. Let v be a unit vector tangent to the unit circle at z0. Then the directional derivative of h in the direction v is just Dv h = < h, v>. If this dot product were positive, then h increases as I move along the unit circle in the v direction, contradicting the fact that h is maximized at z0. Similarly, if it were negative, h would increase in the opposite direction. So we must have < h, v>. If this dot product were positive, then h increases as I move along the unit circle in the v direction, contradicting the fact that h is maximized at z0. Similarly, if it were negative, h would increase in the opposite direction. So we must have < h, v> = 0, i.e., h, v> = 0, i.e.,  h is perpendicular to the unit circle at z0. h is perpendicular to the unit circle at z0.
This is a special case of the Lagrange multiplier method. If we want to maximize f given the constraint g=0, then  f must be perpendicular to the level curve g=0, so it must be a scalar times f must be perpendicular to the level curve g=0, so it must be a scalar times  g, i.e., g, i.e.,  f = f =   g. g.
|
|
 IP Logged IP Logged |
|
|
|
TJMann
Newbie


Posts: 18
|
 |
Re: Analytic problem
« Reply #21 on: Mar 25th, 2008, 3:55pm » |
 Quote Quote  Modify Modify
|
Thx. I see. I thought you were just speaking in general but see that you were referring to the particulars of the given problem.
|
|
 IP Logged IP Logged |
|
|
|
Nourhan
Newbie


  
Gender: 
Posts: 1
|
 |
Re: Analytic problem
« Reply #22 on: May 21st, 2014, 5:50pm » |
 Quote Quote  Modify Modify
|
You have to use Schwarz Equation !
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register