 Author
Author |
Topic: double integral and essential singularity (Read 6481 times) |
|
immanuel78
Newbie



Gender: 
Posts: 23
|
 |
double integral and essential singularity
« on: Dec 27th, 2006, 12:05am » |
 Quote Quote  Modify Modify
|
Let f be analytic in the region G={z:0<|z-a]<R}.
Show that if f has an essential singularity at z=a, then [double integral in G] |f(x+iy)|^2 dxdy = (infinity).
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: double integral and essential singularity
« Reply #1 on: Jan 17th, 2007, 10:45am » |
 Quote Quote  Modify Modify
|
This hasn't be responded to for awhile, and I want to try out towr's new script for inserting math symbols on a real problem, so I thought I'd give my current thoughts on it.
I would suggest assuming that   G |f(x+iy)|2 dxdy < G |f(x+iy)|2 dxdy <  . From this, you ought to be able to show that limz . From this, you ought to be able to show that limz a (z - a)nf(z) = 0. By the Riemann condition, that implies f has a pole of order a (z - a)nf(z) = 0. By the Riemann condition, that implies f has a pole of order  n at a. n at a.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Ghost Sniper
Senior Riddler
   

Do not hide. It is useless.
Gender: 
Posts: 599
|
 |
Re: double integral and essential singularity
« Reply #2 on: Jan 18th, 2007, 10:29am » |
 Quote Quote  Modify Modify
|
on Jan 17th, 2007, 10:45am, Icarus wrote:This hasn't be responded to for awhile, and I want to try out towr's new script for inserting math symbols on a real problem, so I thought I'd give my current thoughts on it.
|
|
So how do you insert the math symbols?
|
|
 IP Logged IP Logged |
*sob* I miss my mommy... *blows nose* huh, I'm on? oh right.
(thinks to self) Time for my speech to these college kids.
"Reason is more important than all emotions..."
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: double integral and essential singularity
« Reply #3 on: Jan 18th, 2007, 11:08am » |
 Quote Quote  Modify Modify
|
on Jan 18th, 2007, 10:29am, hiyathere wrote:| So how do you insert the math symbols? |
|
To save another thread from going offtopic, I've summarized it here
|
| « Last Edit: Jan 18th, 2007, 11:09am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: double integral and essential singularity
« Reply #4 on: Jan 29th, 2007, 11:07am » |
 Quote Quote  Modify Modify
|
Okay - here is an approach that seems to work - though I doubt it was the intended solution:
To ease the notation, we can assume wlog that a = 0. Assume the integral is finite. Express it in polar coordinates:  0 0  0 0 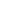 |f2(re |f2(re 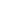 )| rd )| rd dr. For the outer integral to exist, the inner integral must be finite for almost all values of r. Again wlog, we can assume that it is finite for r = R. Now taking the circle of Radius R about 0 as the path, | dr. For the outer integral to exist, the inner integral must be finite for almost all values of r. Again wlog, we can assume that it is finite for r = R. Now taking the circle of Radius R about 0 as the path, |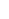 f2 dz | f2 dz |  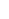 |f2| |dz|, which is exactly the inside integral. Therefore |f2| |dz|, which is exactly the inside integral. Therefore 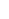 f2 dz is finite. Define F(w) = f2 dz is finite. Define F(w) = 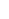 zf2(z)/(z-w) dz. We see that F(w) is finite at all points inside the circle, including 0. F(w) is also holomorphic (a common lemma used in proving Cauchy's formula), and in fact, F(z) = zf2(z) + a for some constant a. This shows that f2(z) can have at most a pole of order 1 at 0. But it is easy to show that if f2 did have a pole at 0, the double integral would be infinite. Hence f2 is analytic at 0. So f is the square root of an analytic function, and hence f has a removable singularity at 0, or has 0 as a branch point. But the latter condition is impossible, since f is analytic everywhere in G. Therefore f must have a removable singularity. zf2(z)/(z-w) dz. We see that F(w) is finite at all points inside the circle, including 0. F(w) is also holomorphic (a common lemma used in proving Cauchy's formula), and in fact, F(z) = zf2(z) + a for some constant a. This shows that f2(z) can have at most a pole of order 1 at 0. But it is easy to show that if f2 did have a pole at 0, the double integral would be infinite. Hence f2 is analytic at 0. So f is the square root of an analytic function, and hence f has a removable singularity at 0, or has 0 as a branch point. But the latter condition is impossible, since f is analytic everywhere in G. Therefore f must have a removable singularity.
Taking the contrapositive gives that if f has a non-removable singularity at a, the integral must be infinite.
|
| « Last Edit: Feb 2nd, 2007, 7:32pm by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: double integral and essential singularity
« Reply #5 on: Feb 2nd, 2007, 4:54pm » |
 Quote Quote  Modify Modify
|
on Jan 29th, 2007, 11:07am, Icarus wrote:| For the outer integral to exist, the inner integral must be finite for almost all values of r. |
|
This can't be enough to show that f doesn't have an essential singularity. Indeed, if f is any function continuous on {0<|z|<R}, then the inner integrals will all be finite, as the integral of a continuous function over a compact interval.
In fact, if f(z) = e1/z - 1/z, then 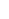 |z|=r f2(z) dz = 0 for all r>0. |z|=r f2(z) dz = 0 for all r>0.
Quote:Define F(w) = 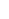 zf2(z)/(z-w) dz. We see that F(w) is finite at all points inside the circle, including 0. F(w) is also holomorphic (a common lemma used in proving Cauchy's formula), and in fact, F(z) = zf2(z) + a for some constant a. zf2(z)/(z-w) dz. We see that F(w) is finite at all points inside the circle, including 0. F(w) is also holomorphic (a common lemma used in proving Cauchy's formula), and in fact, F(z) = zf2(z) + a for some constant a. |
|
F(z) is holomorphic, but only because it is the regular part (nonnegative powers in z) of the Laurent series for zf2(z).
The key to solving the problem is to consider the Laurent series of f:
f(z) =  n=- n=- 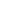 an zn, an zn,
converging absolutely and uniformly on compact subsets of 0<|z|<R. Then we have
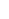 |z|=r |f(z)|2 d |z|=r |f(z)|2 d = 2 = 2  |an|2 r2n, |an|2 r2n,
by orthogonality of the functions {e  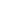 : n : n   }. So }. So
  |f(z)|2 dxdy |f(z)|2 dxdy
=  0R r 2 0R r 2  |an|2r2n dr |an|2r2n dr
= 2   =- =- 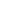 |an|2 |an|2  0R r2n+1dr, 0R r2n+1dr,
which can only be finite if an=0 whenever n<0, that is, if f actually has a removable singularity at 0.
Of course one needs to check that things converge appropriately to justify interchanging the order of integration and summation, but this boring.
|
| « Last Edit: Feb 2nd, 2007, 5:01pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register