 Author
Author |
Topic: About the pole (Read 4312 times) |
|
immanuel78
Newbie



Gender: 
Posts: 23
|
 |
About the pole
« on: Dec 9th, 2006, 5:05am » |
 Quote Quote  Modify Modify
|
Let f be analytic in G={z:0<|z-a|<r} except that there is a sequence of poles {a_n} in G with a_n -> a.
Show that for any w in C there is a sequence {z_n} in G with a=lim z_n and w=lim f(z_n)
|
| « Last Edit: Dec 9th, 2006, 5:06am by immanuel78 » |
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: About the pole
« Reply #1 on: Dec 9th, 2006, 7:00am » |
 Quote Quote  Modify Modify
|
If there is a sequence of poles converging to a, then a is an essential singularity of f. By Weierstrass, the image of any neighborhood of an essential singularity is dense in C. Hence such a sequence must exist.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
immanuel78
Newbie



Gender: 
Posts: 23
|
 |
Re: About the pole
« Reply #2 on: Dec 9th, 2006, 7:29am » |
 Quote Quote  Modify Modify
|
But z=a is not an isolated singularity of f.
Hence z=a is not an essential singularity of f.
|
| « Last Edit: Dec 9th, 2006, 7:30am by immanuel78 » |
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: About the pole
« Reply #3 on: Dec 9th, 2006, 12:57pm » |
 Quote Quote  Modify Modify
|
Consider g(z) = 1/(f(z) - w). In many ways, poles are not really a failure of the function to be analytic.
|
| « Last Edit: Dec 9th, 2006, 1:27pm by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
immanuel78
Newbie



Gender: 
Posts: 23
|
 |
Re: About the pole
« Reply #4 on: Dec 11th, 2006, 10:50pm » |
 Quote Quote  Modify Modify
|
Icarus, may you tell me the way in detail?
I think this problem by usuing your hint but I can't solve it perfectly.
But I can understand this problem more than before because of your hint.
|
| « Last Edit: Dec 11th, 2006, 10:52pm by immanuel78 » |
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: About the pole
« Reply #5 on: Dec 12th, 2006, 4:15pm » |
 Quote Quote  Modify Modify
|
A pole is really just a place where an analytic function takes on the value 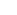 . Around poles, the function is as well-behaved as it is everywhere else. In particular, if you take the inverse, then you get a function that is analytic at that point (there is no such thing as a "removable singularity" - if you ever encounter one, it just means someone has been lazy and not got around to removing it yet). . Around poles, the function is as well-behaved as it is everywhere else. In particular, if you take the inverse, then you get a function that is analytic at that point (there is no such thing as a "removable singularity" - if you ever encounter one, it just means someone has been lazy and not got around to removing it yet).
If f(b) = w for some b in G, then we could just take zn to be any sequence converging to b. So assume that f does not take on the value w. Then g(z) = 1/(f(z) - w) is analytic everywhere in G. the point a is also an essential singularity of g (If it was a pole or removable, then f(z) would have had a worst at pole at a.) Therefore by Weierstrass's theorem, g(G) is dense in C. In particular, for every n, there must be zn in G such that |g(zn)| > n. From this it follows that f(zn) --> w.
(We differ on the definition of essential singularity, by the way - my definition is that any place where analycity fails that is not removable or a pole is an essential singularity, regardless of whether it is isolated. However, Weierstrass's theorem does require an isolated essential singularity - though it can be extended to allow poles by exactly the means I've used here.)
|
| « Last Edit: Dec 12th, 2006, 4:16pm by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register